Na seqüência, apresenta-se o Algoritmo de Thompson para a construção de um autômato finito para reconhecer uma dada expressão regular. Esse procedimento determina como construir um autômato finito não-determinístico para reconhecer sentenças de uma gramática regular. Posteriormente, apresenta-se o procedimento para converter esse autômato para uma máquina determinística.
O primeiro passo do procedimento é decompor a expressão regular que define as sentenças que deverão ser reconhecidas em termos de suas relações elementares:
Uma vez que a expressão regular tenha sido estruturada em termos das relações elementares, é preciso construir um autômato para reconhecer cada uma das partes da expressão. Para cada relação elementar, a estrutura de um autômato correspondente é determinada.
Para reconhecer um símbolo ![]() do alfabeto da linguagem
do alfabeto da linguagem ![]() ,
o autômato correspondente é composto simplesmente por um estado
inicial que atinge um estado final através de uma transição pela
ocorrência do símbolo
,
o autômato correspondente é composto simplesmente por um estado
inicial que atinge um estado final através de uma transição pela
ocorrência do símbolo ![]() (Figura 3.3a).
(Figura 3.3a).
|
[Reconhecimento de um símbolo]
[Concatenação]
[Alternativa]
[Repetição]
|
Se a relação elementar for a concatenação de duas expressões
regulares, ![]() , é preciso compor as duas máquinas
, é preciso compor as duas máquinas ![]() e
e
![]() que reconhecem
que reconhecem ![]() e
e ![]() , respectivamente. Para a máquina
composta, o estado final de
, respectivamente. Para a máquina
composta, o estado final de ![]() é combinado com o estado inicial
de
é combinado com o estado inicial
de ![]() (Figura 3.3b).
(Figura 3.3b).
Para reconhecer a relação elementar que estabelece a alternativa entre
duas expressões regulares, ![]() , a forma de compor as duas
respectivas máquinas
, a forma de compor as duas
respectivas máquinas ![]() e
e ![]() é através da introdução de um
novo estado inicial. Este estado tem transições para os estados
iniciais de cada uma das máquinas
é através da introdução de um
novo estado inicial. Este estado tem transições para os estados
iniciais de cada uma das máquinas ![]() e
e ![]() através da
string vazia. Similarmente, um novo estado final é
introduzido, o qual pode ser atingido com transições pela
string vazia a partir dos estados finais das duas máquinas
originais (Figura 3.3c).
através da
string vazia. Similarmente, um novo estado final é
introduzido, o qual pode ser atingido com transições pela
string vazia a partir dos estados finais das duas máquinas
originais (Figura 3.3c).
A última relação elementar a ser considerada é a repetição, ![]() ,
cuja máquina de reconhecimento deve ser derivada da máquina
,
cuja máquina de reconhecimento deve ser derivada da máquina ![]() que reconhece
que reconhece ![]() . Também neste caso novos estados inicial e final
são introduzidos. Para reconhecer zero ocorrências de
. Também neste caso novos estados inicial e final
são introduzidos. Para reconhecer zero ocorrências de ![]() , há uma
transição pela string vazia direta do novo estado inicial para
o novo estado final. Para reconhecer uma ocorrência de
, há uma
transição pela string vazia direta do novo estado inicial para
o novo estado final. Para reconhecer uma ocorrência de ![]() , há
transições pela string vazia entre o novo estado inicial e o
estado inicial original, assim como entre o estado final original e o
novo estado final. Finalmente, o reconhecimento de várias ocorrências
de
, há
transições pela string vazia entre o novo estado inicial e o
estado inicial original, assim como entre o estado final original e o
novo estado final. Finalmente, o reconhecimento de várias ocorrências
de ![]() dá-se através de uma transição pela string vazia do
estado final para o estado inicial da máquina original
dá-se através de uma transição pela string vazia do
estado final para o estado inicial da máquina original ![]() (Figura 3.3d).
(Figura 3.3d).
A título de exemplo, considere a construção de um
um autômato finito não-determinístico para reconhecer
sentenças descritas pela expressão regular
![]() .
O primeiro passo é decompor a expressão em termos de suas relações
elementares:
.
O primeiro passo é decompor a expressão em termos de suas relações
elementares:
|
|
|
|
|
|
|
|
|
|
||
Uma vez determinadas as expressões regulares elementares que compõem a expressão regular sob análise, é possível construir os autômatos que reconhecem cada uma dessas expressões elementares.
Para reconhecer a expressão ![]() , constrói-se a máquina
, constrói-se a máquina ![]() que
reconhece o símbolo
que
reconhece o símbolo ![]() , usando a construção apresentada na
Figura 3.3a:
, usando a construção apresentada na
Figura 3.3a:
Similarmente, para reconhecer ![]() , constrói-se a máquina
, constrói-se a máquina ![]() que
reconhece o símbolo
que
reconhece o símbolo ![]() :
:
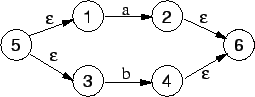
A expressão regular ![]() é a composição pela alternativa das
expressões
é a composição pela alternativa das
expressões ![]() e
e ![]() . O autômato para reconhecer
. O autômato para reconhecer ![]() é
construído pela combinação das máquinas
é
construído pela combinação das máquinas ![]() e
e ![]() conforme a
estratégia apresentada na Figura 3.3c:
conforme a
estratégia apresentada na Figura 3.3c:
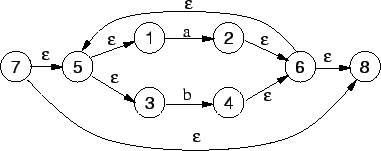
O reconhecimento da expressão regular ![]() é feito pelo autômato
que reconhece zero ou mais ocorrências de
é feito pelo autômato
que reconhece zero ou mais ocorrências de ![]() , ou seja, a máquina
, ou seja, a máquina
![]() é construída a partir da máquina
é construída a partir da máquina ![]() conforme a estratégia
apresentada na Figura 3.3d:
conforme a estratégia
apresentada na Figura 3.3d:
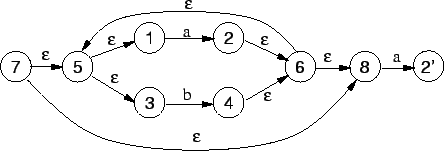
Como a expressão ![]() é formada pela concatenação de
é formada pela concatenação de ![]() com
com
![]() , a máquina
, a máquina ![]() deve combinar a máquina
deve combinar a máquina ![]() com uma
nova instância da máquina
com uma
nova instância da máquina ![]() segundo a estratégia apresentada na
Figura 3.3b:
segundo a estratégia apresentada na
Figura 3.3b:
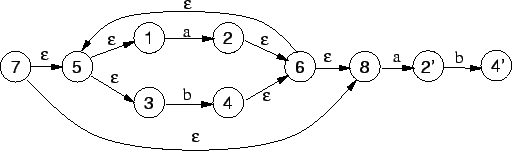
Similarmente, ![]() é uma concatenação de
é uma concatenação de ![]() e
e ![]() .
Combinando a máquina
.
Combinando a máquina ![]() com uma nova instância da máquina que
reconhece
com uma nova instância da máquina que
reconhece ![]() , obtém-se para a máquina
, obtém-se para a máquina ![]() :
:
Finalmente, a expressão completa é uma concatenação de ![]() com
com
![]() . Combinando
. Combinando ![]() com uma máquina
com uma máquina ![]() obtém-se a
máquina que reconhece a expressão regular completa, que é
apresentada na Figura 3.4. Para essa máquina, o estado
inicial é o estado inicial de
obtém-se a
máquina que reconhece a expressão regular completa, que é
apresentada na Figura 3.4. Para essa máquina, o estado
inicial é o estado inicial de ![]() , ou seja, o estado 7, e o estado
final é o estado final de
, ou seja, o estado 7, e o estado
final é o estado final de ![]() , o estado
, o estado ![]() .
.