Hiperbolóide

Um hiperbolóide é uma superfície descrita pelo movimento de um segmento de reta em torno de um eixo de rotação . Cada ponto deste segmento de reta, quando em movimento gera um curva perpendicular ao eixo de rotação. Um hiperbolóide de uma folha é dado pela equação
(x 2 / a 2) + (y 2 / b 2) - (z 2 / c 2) = 1; com a, b e c positivos.

Hiperbolóide reto é um hiperbolóide em que cada curva perpendicular ao eixo de rotação é uma circunferência de raio igual à distância daquele ponto do segmento de reta ao eixo de rotação. É uma primitiva básica suportada pelo pacote PhotoRealistic RenderMan.

Hiperbolóide reto (rib)

Hiperbolóide reto visto de cima (rib)

Hiperbolóide Elíptico (rib)

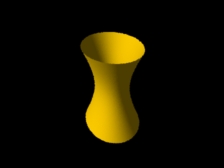Hiperbolóide Elíptico visto de cima (rib)		 Hiperbolóide Elíptico é um hiperbolóide no qual cada curva perpendicular ao eixo de rotação é uma elipse. Escalando-se o hiperbolóide reto com fatores de escalamento diferentes para x e y, pode-se obter um hiperbolóide elíptico com o pacote Photorealistic RenderMan.


Volta para Superfícies Quádricas
Volta para Introdução