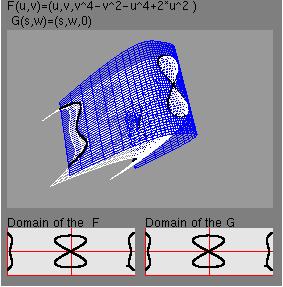
 This project aims at exploiting the differential geometry
techniques in tracing the intesection curve of two regular surfaces.
This project aims at exploiting the differential geometry
techniques in tracing the intesection curve of two regular surfaces.
SSI (Surface-surface intersection) is a fundamental problem in
computational geometry and geometric modeling of complex shapes. The
main motivation of this project is to implement a set of Boolean
operators on free-form boundaries of solid bodies.
There exists a wide variety of methods for surface-surface
intersection computation. They may be classified into six categories:
algebraic, subdivision, continuation, lattice, marching, and hybrid
ones. Algebraic methods rely on the derivation of the equation of the
intersection curve by substituting the parameters of a intersecting
surface into the implicit form of the other. Subdivision techniques
consist in decomposing recursively the surfaces to be intersected into
simpler ones, which allow direct solution such as plane/plane
intersection. Continuation or homotopy algorithms are based on the
idea of finding intersection through a system of differential
equations which ``embed'' the equations of intersecting
surfaces. Lattice approaches reduce the dimensionality of surface
intersections by discretizing one or both surfaces. Marching schemes
generate a sequence of intersection points by stepping from a given
point in a direction that depends on the local differential
geometry. Finally, several algorithms combine two or
more methods to take advantages of them.
Marching-based algorithms comprises three primary phases: hunting
(start point), tracing, and sorting.
- The hunting phase provides
starting point for stepping on the intersection curve. It should
locate all branches of the intersection curve and prevent multiple
copies of the same sequence of points during marching
phase. Hodographs, subdivision techniques, and algebraic methods have
been applied for handling the hunting problem.
- The marching
phase computes sequences of points of an intersection curve branch
by tracing out from the starting points. Incorrect step direction or
size may lead to erroneous results. Most marching methods make use of
curvature analysis or power series expansions about each point of the
intersection curve to control the step. Tracing in the tangent
direction, along a circle, and along a parabola are some solutions
presented in the literature and the curvature dependent step size is
the most used. Differential equation system and continuation method
are also used to trace out a branch of the intersection curve. Even
though, because of the inherent geometric complexity of high degree
algebraic curves that can result from the intersection of two regular
surfaces, intersection curves may have singular points
(self-intersections or cusps), where the normal vectors of the
intersecting surfaces are collinear. In such cases, numerical
solutions may fail or become unreliable.
- The sorting phase
orders the sequences of points into meaningful branches of the
intersection curve. When the points on the intersection curve can be
found sequentially, this sorting is trivial.
Any comments about this project will be very appreciated.
 This project aims at exploiting the differential geometry
techniques in tracing the intesection curve of two regular surfaces.
This project aims at exploiting the differential geometry
techniques in tracing the intesection curve of two regular surfaces.