Árvores

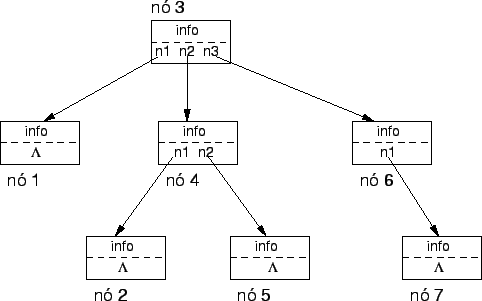
Outra estrutura extensivamente utilizada na programação de sistemas é a estrutura de árvore, que esquematicamente pode ser visualizada como uma extensão de uma lista ligada na qual um nó pode ter mais de um sucessor (Figura 2.5). A representação esquemática de árvores usualmente coloca a raiz no topo, com a árvore crescendo para baixo.

Figura: Representação esquemática de uma estrutura de árvore.

Em uma definição mais formal, uma árvore é uma estrutura que contém um conjunto finito de um ou mais nós, sendo que um dos nós é especialmente designado como o nó raiz e os demais nós são particionados em 0 ou mais conjuntos disjuntos onde cada um desses conjuntos é em si uma árvore, que recebe o nome de sub-árvore.

É possível descrever a árvore representada na Figura 2.5 através da aplicação dessa definição como se segue. A árvore $T$ tem o nó raiz $n3$ e as sub-árvores $T_1$, $T_2$ e $T_3$. A sub-árvore $T_1$ tem o nó raiz $n1$ e não contém sub-árvores; sub-árvore $T_2$ tem o nó raiz $n4$ e sub-árvores $T_4$ e $T_5$; e a sub-árvore $T_3$ tem o nó raiz $n6$ e sub-árvore $T_6$. No próximo nível, as sub-árvores $T_4$, $T_5$ e $T_6$ têm respectivamente os nós raízes $n2$, $n5$ e $n7$ e não têm sub-árvores.

O número de sub-árvores de um nó é o grau do nó. No exemplo, o nó $n3$ tem grau 3; $n4$, 2; e $n5$, 0. O grau da árvore é o maior valor de grau de nó entre todos os nós da árvore; no exemplo, a árvore $T$ tem grau 3. Um nó que não tem sub-árvores, ou seja, cujo grau é 0, é normalmente denominado nó folha da árvore. No exemplo, a árvore $T$ tem folhas $n1$, $n2$, $n5$ e $n7$. Os nós raízes das sub-árvores de um nó são usualmente chamados de nós filhos desse nó, que recebe também o nome de nó pai daqueles nós. Em uma estrutura de árvore, cada nó tem apenas um nó pai.

Um tipo especial de árvore é a árvore binária. Uma árvore binária tem um nó raiz e no máximo duas sub-árvores, uma sub-árvore esquerda e uma sub-árvore direita. Em decorrência dessa definição, o grau de uma árvore binária é limitado a dois. A Figura 2.6 ilustra alguns exemplos de árvores binárias.

Figura: Árvores binárias

Observe na figura que $T1$ e $T2$ são árvores binárias distintas pois, ao contrário da definição genérica de árvores, há diferença de tratamento para a árvore binária entre a sub-árvore direita e a sub-árvore esquerda. Outra diferença de definição para árvores binárias é que elas podem eventualmente ser vazias, algo que a definição de árvore genérica não permite. $T3$ é uma árvore binária degradada, enquanto $T4$ é uma árvore binária completa e balanceada (com sub-árvores de igual tamanho).

Uma das principais aplicações de árvores binárias é a manutenção de estruturas nas quais a ordem é importante. Para manter a ordem dos nós de uma árvore binária, três estratégias podem ser utilizadas:

Pré-ordem

é a estratégia de varredura de uma árvore binária na qual o primeiro nó é o nó raiz, seguido pela sub-árvore esquerda em pré-ordem e finalmente pela sub-árvore direita em pré-ordem;

Intra-ordem

é a estratégia de varredura de árvore binária na qual lê-se primeiro a sub-árvore esquerda em intra-ordem, seguido pelo nó raiz e finalmente pela sub-árvore direita em intra-ordem;

Pós-ordem

é a estratégia de varredura na qual primeiro lê-se os nós da sub-árvore esquerda em pós-ordem, depois os nós da sub-árvore direita em pós-ordem e finalmente o nó raiz.

Aplicando essas estratégias à árvore $T4$ (Figura 2.6), com pré-ordem a seqüência de nós da árvore seria A, B, D, E, C, F, G; com intra-ordem, D, B, E, A, F, C, G; e com a pós-ordem, D, E, B, F, G, C, A.