Representação numérica binária

Inteiros sem sinal têm uma representação computacional (em números binários) equivalente à representação usual para números decimais, ou seja, através da atribuição de pesos associados à posição de cada bit. Grande parte dos computadores atuais utilizam 32 bits para representar números inteiros, o que permite representar $4.924.967.296$ valores distintos. (A geração mais recente de computadores suporta também inteiros com 64 bits.) Uma seqüência binária

$$s_{n-1} s_{n-2} s_{n-3} \ldots s_2 s_1 s_0$$

está associada ao valor inteiro

$$\sum_{i=0}^{n-1} s_i \cdot 2^i$$

onde $s_i \in \{0,1\}$. O bit $s_{n-1}$ é chamado bit mais significativo (MSB), enquanto que $s_0$ é o bit menos significativo (LSB).

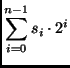
A representação de inteiros com sinal pode usar outros formatos. A forma mais básica é a representação em sinal e magnitude, onde o bit mais significativo denota o sinal associado ao restante da seqüência ( $s_{n-1} = 1$ indicaria que o número é negativo). Este formato tem a desvantagem de ter duas representações diferentes para o valor zero, além de ter circuitos complicados para suportar operações básicas, diferenciando adição de subtração, por exemplo.

Outra formato suportado para representar inteiros com sinal é a representação em complemento de um. A representação para um número negativo neste formato pode ser obtida facilmente a partir da representação do número positivo correspondente simplesmente complementando cada bit da seqüência, ou seja, trocando 0's por 1's e 1's por 0's. Apesar de simplificar circuitos para operações básicas, este formato ainda mantém duas representações distintas para o valor zero.

O formato mais aceito para inteiros com sinal é a representação em complemento de dois. Para obter a representação de um número negativo neste formato, computa-se inicialmente a representação em complemento de um e adiciona-se 1 ao bit menos significativo. Neste caso, o valor inteiro associado à seqüência $s_{n-1} \ldots s_0$ é

$$\sum_{i=0}^{n-2} s_i \cdot 2^i - s_{n-1} \cdot 2^n.$$

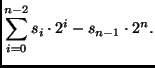
Este formato mantém a simplicidade dos circuitos aritméticos e tem apenas uma representação para o valor zero. Uma característica que lhe é peculiar é o fato de que a faixa de valores representáveis não é simétrica em torno de 0, havendo um valor negativo a mais que a quantidade de valores positivos distintos. Por exemplo, seqüências de cinco bits podem representar valores entre -16 (10000) e +15 (01111).

No formato de representação para números reais, associado ao conceito de notação científica, cada valor (pertencente ao domínio dos reais) é representado por um sinal, uma mantissa e um expoente. Entre as inúmeras combinações possíveis de formatos de representação que seguem esta filosofia básica, o padrão IEEE-754 tem sido o mais aceito e usualmente suportado em hardware (através das unidades de ponto flutuante em co-processadores ou incorporados a CPUs). Este formato suporta representações de números reais em precisão simples (32 bits, dos quais 8 para a representação do expoente e 23 para a representação da mantissa), em precisão dupla (64 bits, sendo 11 para o expoente e 53 para a mantissa) e em precisão estendida (80 bits). Há também representações especiais para os valores $-\infty$, $+\infty$ e NaN (Not a Number, associado ao resultado de operações sem significado matemático, tal como a divisão de zero por zero).

Parece evidente que a representação binária, apesar de ideal para o processador, é de difícil manipulação por humanos. Por este motivo, adota-se usualmente a representação hexadecimal para denotar seqüências binárias.

A vantagem da representação hexadecimal sobre a decimal, que usamos no dia a dia, é a fácil associação com seqüências binárias. A tradução é direta: cada seqüência de quatro bits corresponde a um símbolo hexadecimal. A tabela a seguir define este mapeamento:

binário	hexa	binário	hexa
0000	0	1000	8
0001	1	1001	9
0010	2	1010	A
0011	3	1011	B
0100	4	1100	C
0101	5	1101	D
0110	6	1110	E
0111	7	1111	F

A representação octal também permite um mapeamento similar, de três bits para um dígito entre 0 e 7. Entretanto, a representação hexadecimal também apresenta a vantagem de alinhamento com um byte (8 bits, dois dígitos hexadecimais) e palavras de 16 bits (quatro dígitos).