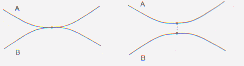Aspectos Implementacionais de Interfaces Gráficas
José Antonio Luján Minchola
Luiz Fernando Stein Wetzel
Curso: IA369J
Professora: Wu Shin Ting
Data: 26/01/2001
Conteúdo
Introdução
3
Capítulo 1
Técnicas de Manipulação Diretas para
Objetos 3D usando dispositivos de
Localização 2D
4
Capitulo 2
Técnicas de arrastre e dispositivos de entrada
3D
9
2.1 Mouse 3D
2.2 Snap-Dragging in Three dimensions
Capítulo 3
Problemas e algumas soluções na manipulação
3D
11
3.1 -Controle de Parâmetros
3.1.1-Problema
3.1.2-Propostas para Resolver o Problema
3.1.3-Deformação de Formas Livres (Free- Form Deformation)
3.1.4-Arame: Técnica de deformação geométrica
3.2-Posicionamento de Objetos Curvos 3D
3.2.1-Problema
3.2.2-Propostas para resolver o Problema
3.2.3-Uma ferramenta interativa para Posicionamento de uma Superfície
Curva sem Penetração
3.3-Controle da Câmera através da Lente
3.3.1-Argumentação matemática da técnica
3.3.2-Movimento da Câmera e velocidade dos Pontos Imagens
Capítulo 4
Arquiteturas para desenvolver interface gráficas
3D 26
4.1 Open Inventor
4.2 An Architecture for an Extensible 3D Interface Toolkit
Bibliografia
29
Introdução
O trabalho em ambientes 3D está longe de alcançar
os muitos recursos disponíveis em ambientes 2D. Atualmente o interesse
para desenvolver técnicas de modelagem e animação
em 3D originaram o surgimento de novas pesquisas nesta área. Podemos
citar duas linhas de pesquisa muito diferentes que abordam o problema do
trabalho em 3D: uma é a realidade virtual, que exige grandes investimentos
em pesquisas; outra é o desenvolvimento de técnicas de manipulação
direta, de visualização de cenas 3D e o aprimoramento de
dispositivos de entrada 3D. Estas técnicas buscam conseguir uma
adaptação natural do usuário acostumado ao ambiente
2D para um ambiente 3D. O presente trabalho comenta e expõe alguns
trabalhos nesta linha de pesquisa.
1. Técnicas
de Manipulação Diretas para Objetos 3D usando dispositivos
de Localização 2D
As técnicas para a entrada de dados em três
dimensões têm permanecido como um problema em computação
gráfica devido à natureza 2D de nossas telas, e dispositivos
de interação mais populares (mouse 2D) . Existem pelo menos
duas correntes de pesquisa que propõe soluções para
este problema: a primeira procura técnicas para que dispositivos
de entrada 2D possam introduzir dados 3D, a segunda tenta desenvolver dispositivos
de entrada 3D. Neste capítulo apresentamos uma técnica que
pertence à primeira corrente.
Esta seção é baseada no artigo "Direct
Manipulation Technique for 3D Objets Using 2D Locator Devices" [G.N. and
D.O].
As técnicas de interação a serem
introduzidas requerem unicamente de um locator bidimensional e um
dispositivo de evento. Além disso, estas técnicas tentam
corrigir as principais deficiências de outras técnicas similares
que são:
a) Elas são indiretas em natureza, isto
é, o usuário, na interação, manipula algum
objeto de controle precisando depois fornecer mais uma especificação
para realizar a manipulação desejada. Por exemplo: uma técnica
indireta é selecionar um eixo de rotação ortogonal
à direção do observador e logo indicar a magnitude
da rotação pelo movimento do locator de cima para abaixo.
b) O feedback que é fornecido, exceto na
manipulação de objetos para si próprio, é bidimensional
tentando simular um feedback tridimensional. Por exemplo podemos fazer
manipulações bidimensionais sobre o topo, frente e lados
visíveis de um objeto e assim dar a aparência de manipulação
em três dimensões.
Uma técnica desejável deveria ser manipular
diretamente a projeção perpectiva de um objeto ao longo dos
três eixos de uma forma natural. Em duas dimensões pode-se
transladar um objeto pela seleção e arrastre deste. Técnicas
análogas são possíveis para manipular diretamente
a rotação e escalamento em duas dimensões. Tais manipulações
naturais não podem ser extendidas a três dimensões
porque existe o problema de especificar a componente z com um único
dispositivo 2D.
Especificando um ponto 3D
Para especificar um ponto no espaço (3D) usa-se
técnica chamada tripla (triad) do mouse. Usando um dispositivo locator
2D manipula-se a posição 3D da tripla do mouse para obter
um comportamento parecido a um mouse 3D. Existem duas etapas deste problema:
Um feedback apropriado para localização 3D e o mapeamento
de movimentos do mouse 2D para mudar a posição 3D.
-Feedback da posição: Com a tripla do mouse
pode-se usar a estrutura do cubo, o qual rodea o espaço de trabalho,
como estrutura de referência. A figura 1 mostra uma tripla do cursor
simples. Existem outras triplas de cursor (ver [G.N. and D.O.]).
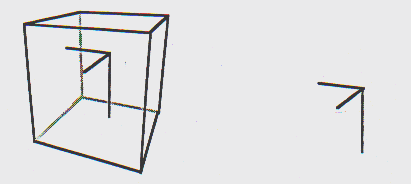
Figura 1
Uma tripla do mouse com e sem a estrutura do cubo
-Mapeamento de movimentos 2D para 3D: para mapear os movimentos
de um locator 2D sobre um movimento 3d usa-se a projeção
bidimensional de um eixo da tripla com o vetor mudado pelo locator 2D (Dx,
Dy) como mostra a figura 2:
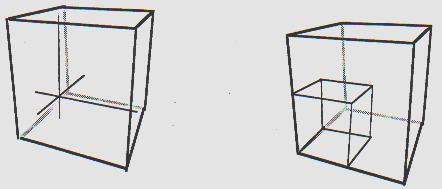
Figura 2 Figura 3
Cursor do espaço Cursor do cubo
Estas projeções fornecem os vetores da tripla
(Xx,Xy), (Yx,Yy), (Zx,Zy). O movimento do mouse 3D ao longo de um dos eixos
esta relacionado à proximidade do movimento do locator (Dx,Dy) ao
eixo de projeção . A correlação entre a mudança
do vetor e um dos vetores da tripla é o coseno do ângulo entre
eles. A direção 3D do movimento é
D=[cos(X),cos(Y),cos(Z)];
onde cos(A) é o coseno do ângulo entre o
vetor da tripla A e o vetor mudado. A nova posição 3D corrente
do cursor é
C=C+p D/ || D ||,
onde p é um fator de precisão o qual controla
a relação entre os movimentos do locator e movimentos
3D reais.
Esta abordagem tem um problema quando o movimento é
unicamente ao longo de um único eixo pois as projeções
sobre os outros eixos não é zero pois sempre existe pequenos
deslocamentos com respeito aos eixos. Neste caso uma das formas de eliminar
estes deslocamentos indesejáveis é permitir só o movimento
ao longo do eixo com valor absoluto máximo.
Translações 3D
Para fazer uma translação, rotação
ou escalamento em 3D temos novamente o problema de como mapear controles
2D numa manipulação 3D. Para conseguir este objetivo faremos
proveito da geometria do objeto manipulado de modo que mantenha uma ou
mais dimensões constantes enquanto manipulamos as outras.
Na especificação de translações
2D escolhe-se um ponto P1 e um segundo ponto P2. A translação
é assim P2-P1. Pode-se estender estas noções para
3D usando P1 para selecionar uma lado ou uma aresta do objeto a ser manipulado.
Na figura 4 o ponto P1 é usado para selecionar a aresta do objeto
cuja projeção 2D esta mais próxima deste ponto. Isto
é uma seleção 3D simples de um segmento de linha.
P1 é logo projetado sobre esta mesma aresta para o ponto P1'. O
ponto P2 é também projetado sobre esta mesma aresta para
o ponto P2'. A translação assim especificada é P2'-P1'
em 3D. Isto tem o efeito de limitar a translação para um
único eixo pela aresta selecionada.
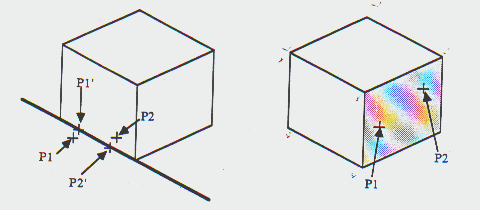
Translação ao longo de uma aresta Translação
sobre o plano
Figura 4
Figura 5
A figura 5 usa P1 para selecionar o lado do objeto. O
ponto P1 (2D) é projetado sobre o plano do lado selecionado para
um ponto P1 (3D). O ponto P2 (2D) é analogamente projetado sobre
este mesmo plano para um ponto P2' (3D). Outra vez a translação
é P2'-P1'.
A figura 6 mostra a translação usando a
tripla do mouse pela escolha dos eixos naturais do objeto selecionado,
de preferência com os eixos coordenados do mundo como os vetores
projeção para o controle dos movimentos do mouse.
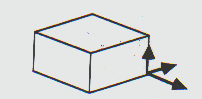
Translaçao usando a tripla do mouse
Figura 6
Rotação 3D:
As técnicas 3D para rotação em duas
dimensões requerem três pontos como mostra a figura 7.
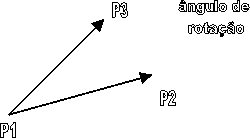
Rotação 2D com 3 pontos
Figura7
Analogamente à translação 3D, usamos
informação do objeto para fazer a manipulação.
Considerar uma rotação 3D como acontecendo
num plano particular sobre um eixo facilita a técnica. A figura
8a mostra a rotação sobre uma aresta.
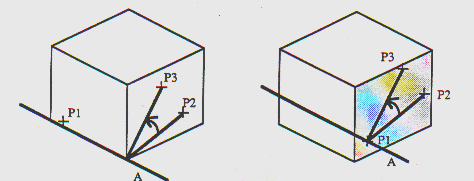
Rotação de arestas Rotação de um lado do cubo
Figura 8a
Figura 8b
P1 seleciona uma aresta A a qual torna-se o eixo de rotação.
Além do eixo de rotação, o ângulo de rotação
é requerido. O ponto P2 (2D) é projetado sobre a superfície
do objeto para obter um ponto P2' (3D). O ponto P3 é projetado sobre
a superfície do objeto para obter um ponto P2' (3D). O ponto P3
é projetado para um ponto P3' (3D) sobre o plano P o qual contém
P2' e tem a A como normal. O ângulo de rotação é
o ângulo entre P2' e P3'.
A figura 8b mostra uma técnica similar baseada
sobre um lado de um objeto. P1 seleciona o lado e é projetado sobre
este para formar P1'. O vetor normal para o lado e P1' são usados
para computar o eixo de rotação A e o lado em si próprio
define o plano de rotação P. Os pontos P2 e P3 são
também projetados sobre o plano de rotação para formar
P2' e P3'. A rotação real é calculada de forma similar
à técnica da aresta da técnica de Rotações
continuas também são possíveis pelo uso do plano e
eixo iniciais selecionados como base para cada rotação incremental.
Escalamento 3D
As dificuldades para escalamento 3D aumentam em realção
à translação 3D e rotação 3D, devido
basicamente de que escalamento não é invariante por rotações.
A figura 10a mostra uma simples técnica que é adaptação
da técnica de translação de aresta.
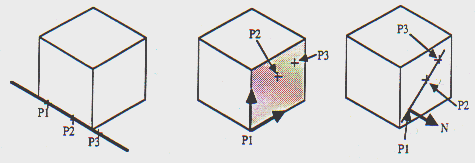
Escalamento usando a aresta Escalamento com dois raios Escalamento uniforme
Figura 9a
Figura 9b
Figura 9c
Pontos P1,P2 e P3 são projetados sobre a aresta
menos distante. O objeto é logo escalado ao longo do eixo definido
pela aresta, usando o fator de escala de (P3'-P1')/ (P2'-P1') ou o escalamento
do P2' para P3' enquanto leva P1' sem mudanças.
A figura 9b mostra as técnicas de escalamento baseadas
sobre dois raios 3D. Na implementação usa-se duas arestas
adjacentes para o vértice mais próximo a P1. Estes raios
definem um plano sobre o qual P2 e P3 são projetados como P2' e
P3'. A transformação T é calculada a qual deve transformar
os dois raios para os eixos X e Y respectivamente e posicionar o vetor
normal sobre o eixo Z. Um próximo calculo P2''=P2'*T e P3''=P3'*T.
Um escalamento bidimensional S é calculado para X e Y usando P3''/P2''
como fator escala. A transformação completa é T*S*T-1.
Esta técnica de escala não é efectiva se os dois raios
não são relativamente perpendiculares.
A figura 9c mostra uma técnica de escalamento uniforme
a qual seleciona a face com P1 e projeta P2 sobre este. P3 é projetado
sobre a linha passando através de P1' e P2' produzindo P3'. A transformação
T é calculada a qual fornece o vetor normal do lado do eixo Z, P1'
para a origem e P2' para o eixo positivo X. O fator de escalamento P3''X
/ P2''X é aplicada em ambos X e Y para um escalamento
uniforme S. A transformação completa é, então
, T*S*T-1.
2. Técnicas arrastre e dispositivos de entrada
3D
2.1-Mouse 3D
Uma grande barreira para o desenvolvimento de interfaces em 3 dimensões
são os dispositivos de entrada e saída. Os dispositivo de
entrada gráficos que estamos acostumados a usar, mouse, mesa digitalizadora,
touch pad,
touch, screen, ... operam apenas em um plano. Para navegarmos em
um espaço tri-dimensional precisamos usar algum artifício
para mapear de 2D para 3D, o que em geral não é fácil
para qualquer usuário assimilar.
Uma forma de melhorarmos esta situação é desenvolvermos
dispositivos de entrada que tenham 3, ou mais, graus de liberdade, sendo
assim próprios para navegação em um espaço
3D.
Para que um novo tipo de mouse tenha sucesso, uma alguns fatores devem
ser levados em consideração:
-
Compatibilidade com os dispositivos 2D. Dificilmente um dispositivo
de navegação em 3D terá sucesso se ele tambem não
for adequado para navegação em 2D. O ideal é que quando
o usuário estiver em um ambiente 2D ele consiga usar seu novo mouse
3D como ele estava acostumado a usar o antigo mouse 2D.
-
O uso do mouse em um ambiente 3D deve ser fácil de
aprender e fácil de operar.
Um exemplo de mouse com mais de 2 graus de liberdade é o Rockin?Mouse
desenvolvido por pesquisadores do Departamento de Ciência da Computação
da Universidade de Toronto. Este mouse apresenta 4 graus de
liberdade, o que o torna bastante recomendado para seu uso
em interfaces 3D.
O Rockin?Mouse é muito parecido com um mouse comum, só que
a sua base é arredondada, permitindo assim 2 graus de liberdade
através do movimento de rotação. A sua utilização
em ambientes 2D é exatamente igual a
um mouse convencional, há um sensor de posição
que permite que a posição do mouse seja mapeada para o espaço
de trabalho. Quando se usa o mouse em um ambiente 3D, além do deslocamento
na mesa, a rotação em torno de
um dos eixos serve para movimentar o cursor.
Um teste de arrasto (arrastar um objeto para uma nova posição)
foi feito com um público com diferentes experiências em manipulação
de objetos em ambientes 3D. O resultado foi que o aprendizado é
bastante rápido e a
eficiência atingida é alta quando comparada ao uso de um mouse
comum, mapeando 2D em 3D através de alguma técnica de chaveamento.
Outros dispositivos de entrada estão sendo desenvolvidos, de forma
que já existem boas soluções para este problema.
2.2-Snap-Dragging IN Three Dimensions
Snap-dragging é uma ferramenta de construção
de objetos tridimensionais baseada em funções de gravidade.
A idéia é que normalmente, quando se está construíndo
uma figura
geométrica, perdemos muito tempo em tarefas de alinhamento de arestas,
planos e posicionamento correto de partes do objeto. Estas tarefas podem
ser bastante simplificadas se
houver funções de gravidade que acelerem o posicionamento
das estruturas nas posições desejadas.
Muitos editores utilizam funções de gravidade para atrair
pontos para vertices, arestas, superfícies. Quando o cursor está
suficientemente próximo de uma destas estruturas, ele
é atraído por ela dando uma impressão de gravidade.
O snap-dragging possui funções de gravidades para os três
elementos citados e estas atuam simultaneamente, sendo que a
região de atuação e a ordem de prioridade é
configurada pelo usuário.
Antes de criar o snap-dragging, o mesmo autor definiu uma forma de rotacionar
objetos baseada em dois objetos auxiliares, os skitters e os jacks. O jack
define o eixo de rotação, o
skitter é um cursor especial que ajuda a posicionar o jack e a definir
a posição inicial e final da rotação. O snap-draging
simplificou este mecanismo utilizando a função de gravidade
também para movimentos de rotação. Existe no snap-drag
apenas um jack, chamado agora de anchor que trabalha junto com os objetos
de alinhamento. Como nesta ferramenta, todas
as intersecções entre superfícies ou linhas são
calculadas automaticamente e funções de gravidade são
atribuídas a elas. São elas que devem ser utilizadas na movimentação
do
skitter.
O snap-dragging aplica funções de gravidade aos vértices,
arestas e superfícies simultanemante. Quando o skitter não
está no domínio de gravidade de um vértice, ele será
atraído
por uma aresta. Se também não estiver no domínio de
uma aresta então será atraído para uma superfície.
Se não estiver no domínio de uma superfície então
o skitter será atraído
por um plano default paralelo à tela.
A orientação do skitter é dependente da orientação
da face ou aresta que o atraiu. Quando o skitter é atraído
por um vértice, sua orientação depende da orientção
das arestas e faces
que determinam este vértice.
O snap-dragging calcula em tempo real todas as intesecções
entre objetos de alinhamento e atribui funções de gravidade
a estas intersecções. Os objetos utilizados são retas,
planos e
esferas.
Para criar objetos de alinhamento primeiramente deve-se selecionar os objetos
da cena que serão utilizados na criação dos objetos
de alinhamento. Através de um comando todos
os vértices dos objetos selecionados se transformam em hot
points, que são desenhados como grandes quadrados brancos. Em seguida
ativa-se um valor no menu de alinhamento,
fazendo com que em cada hot point sejam criados os objetos de alinhamento
especificados para cada um dos valores ativos.
Objetos de alinhamento são desenhados como linhas finas cinza, e
suas intersecções como linhas finas pretas. O algoritmo de
remoção de linhas ocultas não é aplicado aos
objetos
de alinhamento, para que possam ser usados mesmo em situações
onde normalmente estariam escondidos. Apesar de serem usadas linhas finas,
deve-se tomar o cuidade de criar
apenas os objetos de alinhamento necessários, para evitar que a
cena fique muito poluída com estes objetos e suas intersecções.
Existe um objeto especial chamado anchor, cujo
centro é sempre um hot point.
Todas as tranformações dos snap-dragging seguem o skitter.
Como os skitters são atraídos pelos objetos da cena e de
alinhamento, as transformações podem são feitas de
forma
precisa. As transformações disponíveis são:
translação, escalamento, rotação em torno de
um ponto e rotação em torno de um eixo.
De forma geral, os snap-dragging permite que façamos construções
em 3D da mesma forma que fazemos construções planas usando
régua, compasso, esquadro e transferidor.
Nesse sentido ele é apenas um kit de ferramentas de
desenho, que auxilia as pessoas que conhecem o processo de construção
geométrica a criar seus objetos, porém é de pouca
utilidade para usuários que não possuam este conhecimento.
3. Problemas e algumas soluções na manipulação
3D
3.1-Controle de Parâmetros
Na modelagem e animação de objetos (curvas,
superfícies e sólidos) um dos grandes desafios é o
controle dos parâmetros envolvidos, isto é, os parâmetros
relacionados à geometria do mesmo e ao seu posicionamento no espaço.
Parâmetros que possibilitem controlar a forma, esticar, curvar, torcer,
rotacionar e translandar de forma intuitiva, com realismo visual e com
uma boa eficiência de tempo.
3.1.1-Problema
"Obter um modelo para deformação de objetos 3D que
permita controle do parâmetros de forma intuitiva e com realismo".
3.1.2- Prospostas para Resolver o Problema
As técnicas de deformação de objetos, até
então apresentadas pela comunidade que se interessa em solucionar
ou propor soluções parciais para o mesmo, podem ser classificadas
como:
-
Geometria: Que levam em consideração
apenas conceitos e propriedades geométricas.
-
Físicas: Levam em consideração conceitos e propriedades
físicas.
-
Híbridas: Mistura as duas técnicas anteriores, tentando aproveitar
o que há de melhor em cada uma. Exemplos destas técnicas
são
3.1.3 Deformação de Formas Livres (Free-
Form Deformation)
É uma técnica de deformação de objetos geométricos.
Esta técnica reflete muito bem a dificuldades inerentes ao nosso
problema como veremos a seguir:
Em 1986, Sederberg propôs um modelo de deformação
denominado FFD, no artigo Free-Form Deformation of Solid Geometric Models
[T.S. and S.P.], onde um objeto é imerso numa LATTICE (treliça)
de pontos de controle. Em seguida, define-se uma função que
relaciona os pontos de controle e o objeto. Para a obtenção
da deformação do objeto, manipula-se diretamente nos pontos
de controle da lattice gerando uma mudança dos pontos do objeto,
ou uma deformação do mesmo. Com essa técnica pode-se
criar deformações locais ou globais. A forma mais simples
de lattice é o paralepípedo. Criar outras formas de lattice
que dê um melhor controle da forma desejada para deformação
é embaraçoso e difícil. Para um melhor refinamento
da superfície do objeto é necessário uma grande quantidade
de pontos de controle que tornará mais difícil a sua manipulação
para a obtenção do efeito desejado como também aumentará
o custo de processamento.
Quais pontos e como manipulá-los para obter-se a deformação
desejada? Para objetos simples talvez não seja um grande problema,
mas, para objetos complexos é um problema difícil e em certos
casos sem solução. Segundo Sederberg, não dá
para realizar escalamento (em duas ou menos direções) e curvamento
gerais. Neste artigo, ele usou uma lattice paralepipedal e a função
que relaciona o objeto aos pontos de controle foi "Trivariate Tensor Product
Bernstein Polynomial". Afirma ainda, que a função de deformação
pode ser formulada em termos de outras bases polinomiais, tais como produto
tensorial B-splines ou produto não-tensorial de polinomiais de Bernstein.
Em 1992, no artigo "Direct Manipulation of Free-Form Deformation", W.
Hsu, J. Hughes e Henry Kaufman [W.H., J.H. and H.K.], apresentaram quatro
problemas nas deformações via pontos de controle:
-
a forma exata é difícil de ser encontrada;
-
o posicionamento exato dos pontos do objeto é difícil de
ser encontrado;
-
usuários não familiarizados com splines não compreenderão
o propósito dos pontos de controle e os resultados de seus movimentos;
-
os pontos de controle tornam-se difíceis para manipular quando ocultados
pelo objeto sendo deformado, ou quando existem muitos deles abarrotados
na tela.
Neste artigo, Hungles e Kaufman fazem o processo inverso, o usuário
seleciona um ponto de um objeto e então move-o para uma posição
onde este ponto do objeto deverá estar após a deformação.
Computa-se as alterações necessárias para os pontos
de controle do spline FFD que induzirá esta mudança.
A função de deformação usada é um
"Trivariate B-spline Tensor Product". Segundo eles, têm-se um melhor
controle local e uma garantia da continuidade quando alguns pontos de controles
são movidos. Com esta abordagem, elimina-se a necessidade de exibir
os pontos de controle (e sua lattice de controle associada) e a interface
fica mais transparente, permitindo ao usuário se concentrar em outros
detalhes.
Para Karan Singh e Eugene Fiume, em "Wire: A Geometric Deformation Technique
[K.S. and E.F.], as FFD's são muito proveitosas para deformações
de grosseiras-escala de objetos, podendo ser difícil para uso de
deformações de fina-escala, onde uma forma de lattice de
controle densa e customizada é usualmente requerida. Muitas vezes
é mais fácil deformar a geometria do objeto diretamente do
que manipular lattice densa.
As deformações de eixos, proposto por Coquillart, Lazarus
e Jancene, segundo eles, fornece uma representação mais compacta
na qual uma primitiva uni-dimensional, tal como um segmento de reta ou
curva, é usado para definir uma deformação global
implícita. Nessa técnica, usa-se duas curvas W e R, que inicialmente
são as mesmas, o cálculo do ponto mais próximo e referenciais
de Frenet sobre W e R. Calcula-se os pontos de R mais próximos dos
pontos do objeto. A deformação de um ponto P no objeto é
obtida manipulando diretamente a curva W, ficando a sua cópia R
como referência, e computando a transformação que transforma
o referencial de Frenet no ponto mais próximo de P em R no referencial
de Frenet no ponto correpondente sobre W. Tal deformação
é uma porção da transformação obtida
acima. A proporção é baseada numa interpolação
da distância do ponto mais próximo de P em R, ççP-R(p)çç,
entre dois cortes R in e R out. Esta técnica tem um problema nos
pontos onde a curva tem curvatura nula, pois, nesse caso o referencial
de Frenet não está bem definido. Também, o escalamento,
a rotação e a translação são tratadas
numa só transformação, não são separadas,
dificultando o refinamento da deformação, o tratamento das
distorções e descontinuidades na superfície do objeto.
No artigo "Wire: A Geometric Deformation Technique" (1998),
Karan Singh e Eugene Fiume, propuseram uma técnica de deformação
semelhante a técnica mencionada acima, deformações
de eixo, porém, tratando o escalamento, a rotação
e a translação de forma diferenciada, isto é, separadas.
Explicaremos, a seguir, os detalhes dessa técnica.
3.1.4 Arame: Técnica de deformação
geométrica
Esta seção é baseada no artigo "Wire:
A Geometric Deformation Technique" [K.S. and E.F.]. Aqui uma curva no espaço
é parametrizada no intervalo [0,1].
Definição (Arame): Uma arame (wire)
é uma curva cuja manipulação deforma a superfície
de um objeto associado próximo a mesma. Com mais rigor, uma arame
é uma tupla <W,R,s,r,f>, onde
-
W é a curva paramétrica de forma livre (wire);
-
R é a curva paramétrica de forma livre de referência,
cópia congruente de W;
-
s é um escalar que controla o escalamento em torno
da curva R;
-
r é um valor escalar definindo um raio de influência
em torno da curva R;
-
f é uma função escalar f:[0,¥]®[0,1],
chamada função densidade, tal que f é no mínimo
derivável, com derivada 1ª contínua, e monotonicamente
decrescente satisfazendo
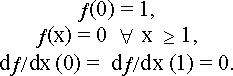
A função f da definição de arame servirá
para definir a função F (fator de atenuação)
que determinará a atenuação da deformação
a medida que os pontos, no volume de deformação de raio r,
se afastam da curva de referência R. Seja p pertencendo a [0,1],
define-se F como
F(P,R) = f (||P-R(p)|| /r),
onde R(p) é o ponto de R mais próximo de
P (se existir mais de um pegue o de menor parâmetro). Observe que
F(P,R) = 0, se P está fora ou sobre a superfície do volume
de compensação, F(P,R) diferente de 0, se P está no
interior do mesmo, e F(P,R) = 1, se P está sobre R.
Quando um objeto é limitado ou demarcado pelo arame,
o domínio de influência do
arame está demarcado pela superfície do
volume de compensação de raio r definida em torno da curva
de referência R. Subsequente manipulação de W resulta
numa mudança entre W e R, que é usada juntamente com F e
s para definir a deformação. A atual deformação
aplicada para um ponto é modulada pela sua influência calculada
quando o objeto estava limitado pela arame.

Figura 1: A arame limitando o objeto
O algoritmo é o seguinte: o objeto O está limitado por
um arame <W,R,s,r,f>, os parâmetros p dos pontos mais próximos
(calcula-se uma vez e só será recalculado caso a curva de
referência mude) e F(P,R) são calculados para cada ponto P
do objeto, isto é, os pontos necessários para construir ou
aproximar uma superfície do objeto, podendo ser um conjunto de vértices
de controle para superfícies de forma livre, um conjunto de vértices
numa polimalha, ou um conjunto desordenado de pontos no espaço.
Para F(P,R) > 0
Escale P como
P(escaldo) = P + [P-R(p)] ×
[1+(s-1)×F(P,R)]
onde P(s) é o ponto P deslocado na direção
do vetor P-R(p).
Rotacione P(s), em torno do eixo de direção dW/dt (p) ×
dR/dt (p), no ponto R(p), de um ângulo q×
F(P,R), sendo q o ângulo entre os vetores
tangente de W e R em p, obtendo o ponto P(rotacionado).
Translade o ponto P(rotacionado) proporcionalmente ao afastamento
entre W(p) e R(p), gerando o ponto deformado P(def)
P(def) = P(rotacionado) + [W(p) -R(p)] ×
F(P,R)
Propriedades:
-
Nenhuma deformação ocorre na criação inicial
do arame W e da curva de referência R, pois W = R e faça como
default r = 0;
-
Pontos exteriores e sobre a superfície do volume de compensação
de raio r da curva de referência não são deformados;
-
Pontos sobre a curva de referência, quando o objeto está demarcado
pelo arame, são deformados e conduzidos ao arame, isto é,
os pontos sobre R transformam-se em pontos sobre W;
-
O fator F(P,R) controla a atenuação da deformação
dentro e fora do volume de compensação, sendo suave e intuitivo;
-
O manipulamento de f fornece controle intuitivo sobre a forma da superfície
do objeto deformado e controla diretamente o grau de continuidade preservado
pela superfície deformada.
Controlando os Parâmetros do Arame
Apesar do uso do fator de atenuação F(P,R) surgem problemas
de descontinuidade da superfície do objeto como, por exemplo, decaimentos
abruptos. Para preservar as propriedades de continuidade da mesma, exige-se
um afastamento suave baseada na região selecionada. Na busca de
solucionar tais problemas, foi proposto o uso de:
-
Locators- posicioana locators ao longo de uma curva de arame e para
cada um define-se r, s e f. Anteriormente, esses parâmetros
eram os mesmos ao longo da curva. Os atributos entre dois locators consecutivos
são obtidos pela interpolação dos atributos dos dois
locators. Obtêm-se um controle local simétrico radialmente
ao longo e em torno de uma curva arame. Locators podem também ser
usados para incorporar transformações não-lineares
como torção, onde eles são usados para controlar o
ângulo de torção ao longo do arame.
F(P,R) = f (|| P-R(pr) ||
/
||R(pr)-D(pd)||),
e para pontos fora do domínio definido pela curva
domínio, pode ser usado o raio de afastamento convencional r. Mas,
surge uma descontinuidade nas vizinhanças de pontos onde cosangle
= 0. Remove-se da seguinte maneira: tome
d Î
(0,1), para cosangle Î [0, d],
F(P,R)= f (||P-R(pr)|| /Interp(cosangle)),
onde Interp dá um valor interpolado suavemente
de r para ||R(pr) -D(pd)||
quando varia de 0 a d.
Múltiplos Arames
Note que um ponto pode pertencer a n volumes de compensações,
isto é, sofrer a influência das deformações
de n arames. A deformação final é a combinação
das deformações de cada arame, da seguinte forma:
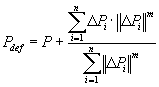 .
.
Propriedades: Para m > 0
-
Numa região onde apenas um arame é relevante, o resultado
é precisamente a deformação de tal arame.
-
Quando vários arames produzem a mesma deformação,
o resultado o resultado é deformação induzida por
qualquer um desses arames.
-
Quando m cresce a deformação do arame de maior magnitude
domina as demais.
-
Em geral, o resultado é uma combinação algébrica
das deformações dos arames individuais, com uma inclinação
(controlada por m) para as deformações de grande magnitude.
-
Quando m é negativo e decresce, a deformação do arame
de menor magnitude domina as demais.
Aplicações
Na modelagem e animação de tecidos e peças de roupas
é importante a criação de dobras e o costuramento
das partes que compõem as roupas. Com esta técnica pode-se
criar dobras desenhando-as como curvas sobre a superfície do objeto
pelo animador ou automaticamente geradas num conjunto de moldes predefinidos.
Para costurar baseado em arame cria-se curvas arame nos lados das superfícies
a ser costuradas, combina-se as mesmas ponto a ponto e reparametriza-se
os lados combinados para um domínio comum, depois da definição
da costura.
Existem outras aplicações não mencionadas neste
resumo mas o leitor pode pesquisá-las no artigo [K.S. and E.F.].
3.2 Posicionamento de Objetos Curvos 3D
O nosso interesse nesta seção é
a tarefa de posicionar objetos criando configurações virtuais.
Por exemplo: numa cena onde empilhamos frutas ou cartas de um baralho para
criar uma pirámide, ou quando queremos reproduzir um copo cheio
de cubos de hielo ou para implementar um quebracabeça 3D.
Entenderemos por posicionamento estável quando os objetos são
posicionados atingindo um grau aceitável de realismo.
3.2.1 Problema:
"Obter um posicionamento estável para objetos paramétricos
curvos 3D sem penetração entre eles e com uma velocidade
boa para ambientes interativos."
3.2.2 Propostas para Resolver o Problema:
Forma Tradicional:
Tradicionalmente, um objeto 3D é
posicionado usando manipulação direta de um mouse, trackball
ou introduzindo um conjunto de dados para a orientação deste
e os parâmetros de translação. O usuário verifica
pela visão quando os objetos não possuem penetração
e estão balaceados fisicamente. Estas técnicas podem ser
cansativas demais para o usuário quando se quer posicionar
objetos curvos, pois as técnicas tradicionais não fornecem
ajuda para atingir uma configuração estável.
Abordagem Física:
Uma alternativa para ajudar ao usuário na tarefa de posicionamento
é aproveitar as vantagens de trabalhos feitos em animação
por computador para criar os movimentos físicos de um objetos. Estas
técnicas pode ser usadas para o problema de posicionamento simulando
movimento através do tempo até que uma posição
estável é atingida. Desafortunadamente nenhuma destas técnicas
é conveniente para posicionamento interativo de formas paramétricas,
não convexa curvas que são as classes que modelos comerciais
mais producem. Uma desvantagem adicional é que o comportamento físico
pode retardar o problema de posicionamento, por exemplo: uma casa feita
de cartas fisicamente tem sempre o perigo de ser destruida quando posicionamos
a próxima carta.
Um Algoritmo de Posicionamento Automático:
O algoritmo proposto por Jhon M. Synder no artigo " An Interative Tool
for Placing Curved Surfaces Without Interpenetration ", produz uma série
(seqüência) de posicionamento do corpo que nunca violam a condição
de não penetração convergindo a um estado estável.
A abordagem neste artigo fornece uma solução parcial do
problema de posicionamento geral de corpos rígidos, um problema
muito difícil para superfícies curvas. Embora a seqüência
de estados não corresponda ao movimento real do objeto, o estado
final representa uma configuração estável de acordo
com às leis de equilibrio das forças estáticas, assumindo
como estando imóveis os corpos não ativos.
Algoritmo de Posicionamento Automático (A.P.A.)
place body in a noninterfering initial state
loop
check for tracked point transitions
compute pseudo-forces at each contact point, and on body
update active body's placement using e (solution
step)
adjust tracked points for new placement
if unable, e =e
/2 and start loop again (loop failure)
while new polygonal collision exists and collisions < Nsimultaneonus
if unable to convert collision to a contact point then
e =e /2 and start
loop again (loop failure)
else
add tracked point
endif
endwhile
if collisions were successfully added, restore old value of e
if objetive function increases, e =e
/2 (loop failure)
if loop was completed successfully, increase e
by e =max(le ,emax)
render current state
complete user interaction requests: interrupt, undo,direct repositioning,
force or parameter change, etc.
until stable
3.2.3-Uma ferramenta interativa
para Posicionamento de uma Superfícies Curvas sem
Penetração
Esta subseção é inteiramente baseada no artigo:
" An Interative Tool for Placing Curved Surfaces Without Interpenetration".
O artigo pressupõe que o problema de posicionamento preocupa-se
com uma rápida produção de configurações
desejadas de objetos e não de como se atingiu estas.
O objetivo das técnicas deste artigo é conseguir um estado
(configuração) estavél de alguns estados arbitrários
criando mudanças que são intuitivas e controlá- veis
mas não necessariamente de precisão física. Para conseguir
este objetivo simula-se a precisão física das seguintes maneiras:
-
Corpo não tem velocidade. De fato não existe noção
explícita de tempo no sistema todo; em vez disso o corpo é
movimentado através de uma série de estados discre- tos,
cada um dos quais obedecem limitações que aseguram a não
penetração de corpos.
-
Em quando forças e torques são calculadas para cada estado,
elas não são a forças reais que um corpo dinámico
experienciaria instantamente. Elas são escolhidas para a rápida
convergência do corpo para um posicionamento estável "próximo",
e são chamadas de pseudo-forças e pseudo-torques.
-
tempo exato quando a transição de pontos de contato acontece
(exemplo: contatos desaparecem) não é calculado. Em vez disso,
transições são feitas depois de cada passo discreto.
-
Pequenos ajustes não físicos são feitos para uma posição
do corpo e orientação de forma a preservar as limitações
de não penetração.
-
Somente um corpo por vez, o corpo ativo, pode ser movido. Quando este corpo
se move, interage com outros corpos os quais se mantem fixos. O usuário
pode mudar o corpo que esta correntemente ativo de forma a para mover corpos
sequencial- mente de posição.
Representação de Superfícies:
Um corpo é um objeto sólido e rigidamente
móvel que interage com outros corpos. Este é representado
por um conjunto de pedaços, cada um dos quais é uma superfície
paramétrica analítica, cuja união contém a
fronteira do corpo. Cada pedaço é definido de forma que os
vetores normais à superfície apontam para o exterior do corpo.
Selecionando uma representação por
pedaços, o problema de detecção de colisão
poligonal é extremamente eficiente mas não pode ser usada
sozinha para achar colisões precisas entre superfícies. Portanto,
usamos uma representação híbrida: uma representação
poligonal é usada para detectar novos pontos de contato que surja
entre corpos, e uma descrição funcional é usada para
ajustar este pontos tal que verdadeiramente pertença à superfície
curva e para rastrear o movimento destes pontos.
A descrição poligonal é uma
malha de triângulo com coordenadas paramétricas (u,v) por
vértices. Cada vértice esta sobre a superfície analítica.
A localização de uma colisão pode então ser
aproximada encontrando a intersecção de triângulos.
A aproximação poligonal também
é usada durante o posicionamento manual para determinar quando um
corpo esta num estado de não interferência, isto é,
quando o objeto não possui contato com nenhum outro objeto depois
de sofrer uma mudança de posição. Quando uma interferência
é detectada, o corpo é feito transparente e um pequeno ponto
é mostrado no ponto de intersecção. Finalmente, a
aproximação poligonal é usada para selecionar um corpo
usando o algoritmo de ray casting.
A descrição funcional para superfícies
paramétricas são criadas com uma linguagem simbólica.
A avaliação de pontos de superfícies e derivadas de
até segunda ordem é requerida. Como as superfícies
analíticas são aproximadas por triângulos, o processo
de detecção de colisão, pode ter duas clases de erros
como mostra a figura 1.
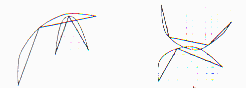
(a)
(b)
Figura1: Colisões inconsistentes
para superfícies analíticas vs aproximação
poligonal.
Quando um destes objetos é côncavo,
a colisão pode acontecer entre aproximações poligonais
mas não na superfície analítica (figura 1a). Esta
é detectada por um erro na iteração numérica.
Uma colisão entre superfícies analíticas pode também
ser perdida com aproximações poligonais (figura 1b).
Existem três vantagens de se usar uma descrição
analítica da superfície curva. Primeiro, uma precisão
muito melhor é atingida. Segundo, ao usar-se a superfície
diferenciável, facilita-se a mudança incremental de um estado
do corpo enquanto se cumpre a condição de não penetração.
Quando um corpo curvo pode continuamente deslizar sobre a superfície
de outro, muitos estados não são atingidos quando a aproximação
poligonal é usada. Terceiro, a convergência rápida
para a estabilidade pode ser atingida. A superfície analítica
fornece os vetores normais exatos nos pontos de contato que não
estão disponíveis na aproximação poligonal.
Detectando Colisões Rapidamente
O autor do artigo aproxima cada corpo por um conjunto
de triângulos, organizados numa hierarquia de caixas limitantes,
particionando o objeto. Nos nós terminais da hierarquia estão
os triângulos, cada um dos quais é marcado com um identificador
(corpo, pedaço). Cada nó da árvore contém uma
caixa limitante na forma (xmin , xmax ,ymin
,ymax , zmin , zmax ). Além disso,
pode conter ou uma lista de nós filhos, ou informação
para um triângulo (no caso de um nó terminal).
Uma hierarquia similar é construida para o
conjunto de corpos no sistema (mundo). Duas formas de detecção
de colisão são requeridas para o posicionamento interativo.
Detecção de colisões simples são computadas
quando um objeto interfere com algum outro objeto, e é usada escolhendo-se
um estado de não interferência do qual começa ou recomeça
convergindo para a estabilidade. Uma segunda forma de detecção
de colisão é usada para computar quando um corpo, que já
está em contato com outros corpos, intersecta-se em alguns pontos
adicionais. Para fazer isto, define-se as esferas de negligência
ao redor dos pontos de contato. Durante a execução do processo
de detecção, colisões potenciais dentro das esferas
de negligência são descartadas. O algoritmo assim localiza
novos pontos de colisão (figura 2).

Figura 2: Esferas de negligência
Construindo a Hierarquia de caixa limitante:
Para construir uma hierarquia de caixa limitante para um corpo, aplica-se
o algoritmo maketree para a lista de triangulos que formam o corpo.
maketree(L)
partition L into set of n list Li
create root node R
for each i, insert maketree(Li ) as child
of R
return R
Em cada chamada de maketree, a caixa limitante para
o nó resultante R é tomada como a união das caixas
limitantes de seus nós filhos. O coração do processo
de construção é a partição de uma lista
de nós L sobre uma sub-lista Li .
Percorrendo a hierarquia da Caixa
Limitante
A detecção de colisão é computada percorrendo-se
a hierarquia da caixa limitante de um par de nós NA e
NB .
Pares de nós de duas hierarquias são examinados em ordem
de profundidade de acordo com o seguinte algoritmo básico.
Traverstrees (NA ,NB)
inicialize stack of active pairs with (NA ,NB)
while stack is nonempty
pop off next pair (A,B)
loop through child nodes of A and B: (Ai Bj)
if (Ai Bj) collide
if both are triangles, record collision
else push pair onto active list
Três tipos de colisão computados acontecem: caixa limitante
vs caixa limitante, caixa limitante vs triângulos e triângulos
vs triângulos. Se ambos nós são não terminais
, uma colisão de caixa limitante vs caixa limitante é realizada
pela transformação da caixa limitante do segundo objeto para
o sistema do primeiro, e testando quando os dois limites sobrepõe-se.
Se só um é deles é terminal, um teste de colisão
de caixa limitante/ triângulo é realizado, novamente no sistema
coordenado do primeiro objeto. Do contrário, um teste para a interseção
de dois triângulos é realizada. Quando dois triângulos
colide, a localização da colisão e o ponteiro para
os dois triângulos são salvados.
Várias mudanças para o algoritmo básico
são necessárias. O primeiro é selecionar nós
baseados sobre uma lista de esferas de negligências. Para fazer isto,
testamos a intersecção da caixa limitante de A e B para conferir
se estam ou não inteiramente no interior de alguma esfera de negligência.
Se isto, acontece descarta-se o par. Também se descarta a colisão
entre triângulo se esta estever contida em alguma esfera de negligência.
A segunda mudança melhora o desempenho: quando uma caixa limitante
do nó é pequena com respeito à outra, não subdivide-se
o nó em filhos, mas se compara este nó sem subdivisão
com os filhos do nó maior.
Computando os pontos de Contato:
A abordagem aqui cria só uma quantidade suficiente de pontos
para prevenir penetração e atingir um estado estável.
Estes pontos são chamados de pontos de interface e consiste de um
par de pontos sobre dois corpos. Pontos de interface são rastreados
(atualizados) quando o corpo move-se de estado para estado usando iteração
numérica.
Dois tipos de pontos de interface são usados: pares de contato
e pares extremais, mostrados na figura 3. Os corpos realmente se contatam
em pares de contato. Forças que equilibra forças externas
tais como gravedade são aplicadas em pares de contato. Estas forças
são unicamente aplicadas para puxar o objeto de alguma forma, para
evitar a penetração, isto é, objetos não se
colam. Quando tal força de colar é obtida esta não
é aplicada mas em vez disso um par de contato muda para extremal.
Pares extremais são pontos sobre um par de corpos a uma distância
mínima, os corpos não contactam numa vizinhança ao
redor de pares extremais. As forças não são aplicadas
em pares extremos.
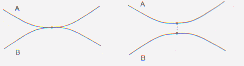
par de contato par extremal
Figura 3
Rastreamento de Contatos:
Depois que o corpo é movido, o algoritmo de posicionamento automático
deve rastrear aos pontos de interface de suas posições previas.
O seguinte algoritmo de rastreamento de duas fases produz excelente estabilidade
numérica.
A primeira fase, chamada a fase de condicionamento. Nesta fase, cada
ponto de interface, representado com um par de posições paramétricas
(u,v), é independemente ajustada para satisfacer as condições
de pontos extremais usando iteração numérica. A condição
inicial para esta iteração é a localização
paramétrica do ponto de interface antes que o corpo for movimentado.
Na segunda fase, chamamos a fase de ajuste de contato, ajustam-se os
parâmetros do movimento rígido do corpo e a localização
de todos os pares de interface preservando as condições de
contato ou extremais. A iteração numérica encarregar-se
simultaneamente de realizar as condições extremais ou de
contato para todos os pontos de interface. Condições iniciais
para esta iteração são o posicionamento corrente de
corpos, e a localização paramétrica dos pontos da
interface depois da fase de condicionamento.
Quando a iteração númerica em cada fase rastreamento
falha, o algoritmo de posicionamento tenta um pequeno movimento do corpo
activo de ser ultimo estado correto (ver A.P.A.).
Deletando as Transições de Contato:
Antes de que um corpo seja movido, o algoritmo de posicionamento verifica
as transições de pontos de contatos. Quando uma transição
é detectada, o ponto de interface é deletado no caso de uma
transição desapareça, ou trocado entre contato e extremal.
As seguintes transições (com suas condições
para acontecer) são detectadas:
-
Extremal-para-contato- Se a distância de separação
entre os corpos torna-se negativa.
-
Contato-para-extremal- Quando forças de contato atraem em vez de
repeler os corpos.
-
Desaparecem os extremais.
-Distância de separação excede o threshold.
-Falha a interação na fase de condicionamento.
-Quando pontos torna-se próximos demais outro ponto de interface.
-Quando pontos caem fora do domínio paramétrico do pedaço.
-Quando pontos caem fora do dominio paramétrico do pedaço.
-Quando pontos torna-se próximo demais para outros pontos de
interface.
O usuário pode opcionalmente desabilitar a transição
contato-para-extremal garantido que o corpo ativo fica em contacto com
o movimento.
Criando Contactos
O algoritmo de posicionamento automático converte pontos de colisão
sobre os corpos poligonais em pontos de contacto sobre superfícies
paramétricas analíticas. Uma série de passos, ilustrada
na figura 4 é feita, cada um dos quais usam os resulta- dos dos
passos prévios como a condição inicial na iteração
numérica:
Passo 1: Interpolar o ponto de colisão poligonal produz um
par de pontos paramétricos (u1 ,v1 ,u2
,v2). O identificador (corpo,pedaço) para cada um dos
triângulos intersectados, permite a recuperação das
funções de superfície apropriadas usadas no seguintes
passos (figura 4a).
Passo 2: Iterar sobre a interseção analítica (figura
4b).
Passo 3: Fazer alguns passos de descida do gradiente para forçar
ao par tornar-se os pontos de penetração maximal (figura
4c). Isto é necessário para que os próximos passos
de iteração esteja na direção correta (isto
é tornar à penetração maximal parecida à
separação maximal). A função objetivo é
definida na seção seguinte na equação 2.
Passo 4: Iterar sobre os pares extremos (figura 4d). Isto é um
passo de condicionamento exatamente parecido à forma de condicionamento
do rastreo.
Passo 5: Iterar sobre um par contacto (figura 4e). neste passo, os parâmetros
de posição do corpo ativo e a localização de
todos os pontos interface são ajustados. Equações
para todos os pontos de interface deve ser satisfeitos simultamente, desde
que o posicionamento do corpo ativo afecte as condições de
contato de pontos de interface prévios.
Observação: Os passos 2,4, e 5 envolvem iteração
numérica a qual pode falhar.
Algumas formas de contornar a falha são dadas no artigo [JMS].
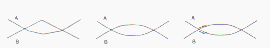
(a)colisão poligonal (b)intersecção analítica
(c)descida do gradiente
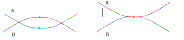
(d)par extremal (e)par de contato
Figura 4: Passos na convergencia de uma colisão poliédrica
sobre um ponto contato
Iteração do Ponto Contato:
Rastreamento de pontos de interface e creação de ponto
de contato usam iteração de Newton sobre um sistema de equações.
Dado um sistema de equações não linear F(x)=0 e um
ponto próximo à solução, x0, uma aproximação
sucessiva para a solução verdadeira, é atingida resolvendo
o sistema linear de equações:
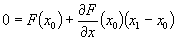 (1)
(1)
onde 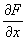 é o jacobiano
de F. Resolvemos o sistema linear (1) usando a descomposição
de valor singular (SDV), o qual permite que sistemas não quadrados
seja resolvidos e é numericamente robusta. O processo é logo
repetido para melhorar a aproximação, produzindo uma sequência
de iterações xi .
é o jacobiano
de F. Resolvemos o sistema linear (1) usando a descomposição
de valor singular (SDV), o qual permite que sistemas não quadrados
seja resolvidos e é numericamente robusta. O processo é logo
repetido para melhorar a aproximação, produzindo uma sequência
de iterações xi .
Só manten-se descritos os sistemas pertinentes das equações
(F da equação 1) e seus parâmetros x,
para cada processo iterativo. Assim teremos dois pontos cada um sobre uma
superfície móvel rigidamente
Si (Qi,
Xi, ui, vi), i=1,2; onde Qi
é uma rotação
em 3D e Xi é uma translação em
3D:
Si(Qi, Xi, ui, vi)
= Qi si (ui,vi)+Xi;
si (ui,vi) representa a superfície
no seu sistema coordenado local. Existem três sistemas de equações
usados na iteração de Newton acima:
-
Interseção [iteração sobre
(u1
, v1 ,u2 , v2)]:
S1 -S2 =0.
O par de pontos paramétricos é movido para tornar-se uma
interseção verdadeira dos corpos, usados no passo 2 da seqüência
de criação de pontos de contato.
-
Extremal [iteração sobre ( u1 , v1
,u2 , v2)]
(S1 -S2 )×N1=0;
N1 +N2=0;
onde N1 e N2 são as normais
unitárias das duas superfícies. Estas condições
implicam que a distância entre o ponto par é um extremo local
(o vetor entre os pontos esta na direção de uma normal da
superfície e duas normais são anti-paralelas). Se os corpos
são separados por uma distância pequena, a iteração
deve causar que os dois pontos se tornem pontos de distância mínima
entre as duas superfícies. Se um corpo penetra, a iteração
deve causar que os dois pontos se tornem pontos de penetração
muito distante. Esta iteração é usada no rastreamento
e no passo 4 da sequência de creação do ponto contato.
-
Contato [iteração sobre ( Q1 , X1
,
u1 ,v1 ,u2 , v2)]
S1-S2=0;
N1 +N2 =0.
Muda-se a posição e orientação do primeiro
corpo com a localização paramétrica do ponto de contacto
em ordem para atingir um ponto de contacto verdadeiro onde as superfícies
toca-se e são tangentes. Esta iteração é usada
no rastreamento e no passo 5 da seqüência de creação
de ponto contato.
Criação de pontos de contato também envolvem iteração
descendente do gradiente no passo 3. A função objetivo cujo
gradiente esta em descida, a função distância de separação
sinalizado G é dado por:
G=(S1 - S2).N1 (2)
Se o corpo não toca-se, esta função
é positiva dentro de uma vizinhança do ponto de separação
máxima. Se os corpos se penetram, a função é
negativa dentro da região de penetração.
Convergindo a uma Configuração Estável
Convergência a um estado estável é atingida pela
aplicação de pseudo-forças que causam uma mudança
incremental na posição do corpo ativo. Usando quantidades
de forças similares conclui-se duas coisas:
-
Estas levam a mudanças no posicionamento do objeto que o usuário
pode prever e produz uma convergência rápida para um posicionamento
estável.
-
Pseudo-forças difierem de forças físicas porque estas
são solucionadas para objetos estáticos e não em movimento
mas são diretamente aplicadas para atualizar a posição
do objeto.
Três classes de pseudo-forças são
usadas: Externas, as quais representam a gravedade e especificações
do usuário, contato as quais são aplicadas em pontos
de contato para o balance de forças externas, e residual,
a qual representa a força resultante (externa-contato) aplicada
para ajustar a posição da posição do corpo.
3.3 Controle da Câmera através
da Lente
Existem muitos modelos de câmera que difierem na quantidade de
parâmetros para especificar a vista 3D (3-D view); a qual é
determinada pelo centro de projeção, o plano de visão
e o volume de recorte.
Os modelos de câmera são inflexiveis. Para mudar o controle,
um deve selecionar um modelo pre-existente diferente ou derivar e implementar
um novo. Se esta inflexibilidade pode ser removida, o esforço dedicado
ao control da câmera pode ser reduzido e a qualidade do resultado
é ressaltada.
Esta seção é baseada no artigo [MG and A.W], o
qual introduz um controle da câmera através do lente, um conjunto
de técnicas que permitem a um usuário manipular uma câmera
virtual através da manipulação direta sobre a imagem.
No artigo, apresenta-se um conjunto de técnicas, denominado como
Controle da Câmera através da Lente, que oferece uma solução
geral para este problema. Em lugar de um conjunto fixo, é fornecido
para o usuário uma paleta de imagem-espaço interativo e controles
cena-espaço. Um exemplo da vantagens do controle é que a
posição imagem-espaço de um ponto cena-espaço
arbitrário pode ser controlado pelo arrastre interativo enquanto
outros pontos são movidos.
Distâncias Imagem-espaço, tamanho e direções
pode ser também controladas. Pontos podem ser restringidos a permanecer
dentro da imagem ou dentro de uma subregião específica. Estes
e outros controles imagem-espaço pode ser livremente combinados
com controles cena-espaço em forma direta sobre a posição
da câmera e orientação.
3.3.1 Argumentação matemática da técnica:
Modelo matemático usado:
Seja p um ponto no espaço da cena a ser projedo na tela
virtual (espaço imagem) e m o ponto imagem correspondente.
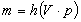
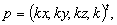
onde h é a função que converte as coordenadas
homogêneas para coordenadas imagem 2D, assim
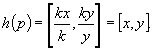
A matriz V representa as transformações de visualização,
que é determinada por um produto de várias matrices cada
uma sendo uma função de um ou mais parâmetros.
V=PRT;
onde RT realizam a mudança do espaço da câmera
para o espaço da cena e P é a matriz de transformação
de perspectiva.
3.3.2 Movimento da Câmera e velocidade dos Pontos Imagens
Assumimos agora que o ponto no espaço cena p é
fixado, logo o ponto imagem m é uma função
dos parâmetros da câmera q. Esta relação é
não linear pois h é não linear, como em geral
é V(q). Obtendo-se a seguinte expressão para a velocidade
da imagem 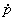 :
:
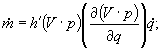
onde 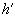 (p) é a matrix
das derivadas de h(x).
(p) é a matrix
das derivadas de h(x).
Fazendo
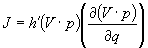
temos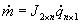 , que é um sistema
linear. Porém J não é quadrada.
, que é um sistema
linear. Porém J não é quadrada.
Um único Ponto de Controle:
Expressando 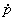 como função
de
como função
de 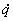 , consideramos agora
o problema de controlar um único ponto imagem, isto é calcular
para um valor de
, consideramos agora
o problema de controlar um único ponto imagem, isto é calcular
para um valor de 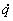 o comportamento
do ponto imagem assumindo uma velocidade dada
o comportamento
do ponto imagem assumindo uma velocidade dada 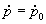 .
.
O problema que agora deve ser resolvido é: Sujeito à restrição
que 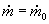 , minimiza-se a desviação
de
, minimiza-se a desviação
de 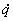 em relação
a um valor especificado
em relação
a um valor especificado 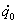 .
Isto é:
.
Isto é:
Minimizar
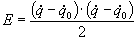
sujeito a 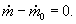
Sob algumas considerações e usando multiplicadores de
Lagrange podemos chegar a:
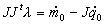
e finalmente
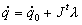
a qual é uma E.D.O. de primeira ordem com
valor inicial.
Com vários Pontos de Controle:
Para s pontos imagem de controle, combina-se
as s equações em uma única.
Logo o sistema para um único ponto
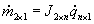
passa a ser
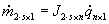
A função objetivo passa ter s
restrições.
Arrastre forçado e controle flexível
Quando controles são acrecentados consecutivamente pelo usuário,
é possivel que surga conflictos. Esta dificuldade pode ser contorneada
pelo uso de um método de mínimos quadrados. Outra solução
proposta no artigo é só permitir ao usuário o arrastre
de pontos e outras características sujeitas a limitações
impostas por controles já existente, assim evitamos os conflictos.
Conseguimos esto incorporando o comportamento desejado do arrastre na função
objetivo.
Assim, por exemplo, um ponto cuja faixa de movimento
é limitada pelos controles move-se livremente até o limite
de trajetoria do mesmo. Uma maneira de implementar o controle "flexível
" é especificar o movimento da câmera desejada
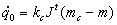 ;
;
onde kc é uma constante
e mc é a posição do cursor na imagem (prévio
ponto de controle).
O valor inicial de q0 pode ser uma estimativa inicial do
usuário.
Realimentação da posição
Acrescentamos um termo de realimentação linear a nossa
expressão inicial do requerimento de controle:
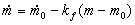
onde kf é uma constante de realimentação
e m0 a desejada posição para m no tempo corrente.
Rastreando um ponto em movimento
Já que p depende agora do tempo, um termo adicional aparece
na nossa equação:
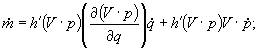
4 Arquiteturas propostas para desenvolver interfaces
gráficas 3D
4.1 Open Inventor
Open Inventor é uma ferramenta para desenvolvedores de aplicações
3D interativas. Seu objetivo é facilitar a criação
de aplicações gráficas 3D que utilizem tanto técnicas
de manipulação direta em objetos 3D, como elementos de interface
2D.
Esta ferramenta oferece uma plataforma extensível para a representação
de cenas 3D, de forma que as aplicações possam integrar seus
dados com objetos gráficos, em vez de utilizarem cópias duplicadas.
Também está incluído um modelo de eventos simples
e integrado que permite a manipulação direta de objetos 3D.
O foco do Open Inventor é a descrição de cenas e sua
utilização em interfaces interativas e não a construção
de objetos 3D. Para este fim existem outras ferramentas e técnicas
abordadas neste trabalho.
Uma ferramenta 3D realmente interativa deve prover uma coleção
rica e extensível de objetos, e deve suportar manipulação
direta, permitindo que os usuários interajam com os objetos na mesma
janela onde eles são exibidos. Isso é uma técnica
comum em 2D que raramente é implementada em ambientes 3D.
O alicerce desta ferramenta é a base de dados de cena. Esta base
de dados armazena a representação dinâmica de cenas
3D na forma de grafos de objetos chamados nós. Várias
classes de nós implementam diferentes geometrias, propriedades e
definem comportamentos quando a base de dados é interpretada. Existem
ações que podem ser aplicadas a uma cena, ou parte da cena.
Existem também objetos que acrescentam animação às
cenas, e outros para rastrear alterações.
São definidas classes de eventos e os nós
smart
para tratar estes eventos. Estas classes definem um conjunto extensível
de eventos abstratos como por exemplo Evento do Botão. Um
exemplo de nó smart é o de Seleção,
que permite que a aplicação mantenha uma lista de objetos
selecionados. Outro nó smart é o manipulador. Este
nó responde a eventos de interação e edita outros
nós da base de dados. Manipuladores oferecem uma maneira fácil
para aplicações incorporarem interação 3D direta.
O Open Inventor não está amarrado a um sistema de janelas
particular. Bibliotecas utilitárias ligam a ferramenta a um sistema
particular de janelas, estas bibliotecas implementam a área de display
e traduzem eventos do sistema de janelas para o ambiente do Open Inventor.
O Open Inventor está implementado em C++, que suporta os paradigmas
de orientação a objeto essenciais para o desenvolvimento
de sistemas extensíveis. Ele utiliza o Open GL como bibliteca gráfica.
Uma cena o Open Inventor é descrita através de um grafo,
onde são colodados diversos nós. Os principais tipos de nós
são: Formas (cone, cubo, cilindro,...); Luz/Câmera (câmera
ortográfica, câmera perspectiva, ponto de luz, ...); Nós
de Grupo (grupo, separador, seleção, ...); Nós de
Propriedades (cor base, estilo de desenho, fonte, ...). A disposição
destes nós indica a ordem que eles serão interpretados para
construir a cena. Um mesmo sub-grafo pode ser interpretados várias
vezes durante a construção de uma cena permitindo um reaproveitamento
do sub-grafo e reforçando aspectos de consistência. Um exemplo
de reaproveitamento de sub-grafo é a representação
de uma bicicleta. Um mesmo sub-grafo pode ser utilizado tanto para representar
a roda da frente como a de trás. Todas as características
específicas de cada uma destas rodas deve estar fora deste sub-grafo
e todas as características comuns devem estar neste sub-grafo.
Objetos de ação interpretam os grafos de cena para
realizar operações específicas, como por exemplo mostrar
a cena na tela, determinar os limites da cena, executar algoritmos de busca,
ou salvar informaçoes em arquivo. Os grafos são normalmente
interpretados da esquerda para a direita, sendo que todos filhos devem
ser resolvidos antes de passar para o elemento direita. O nó separador
é usado para salvar o estado antes que os filhos sejam executados
e restaurar este estado no final da execução do sub-grafo.
Sensores são nós usados para detectar mudanças
de outros nós e implementar animações simples. Os
sensores geram eventos para a aplicação quando o estado que
está sendo monitorado for alterado. Um tipo especial de sensor é
o timer, que avisa a aplicação quando um intervalo
de tempo pré-definido expirou. Este sensor pode ser programado,
por exemplo, para gerar 30 eventos por segundo, para ser usado em animações
de parte da cena.
4.2-An Architecture for an Extensible 3D Interface
Toolkit
Este artigo descreve uma proposta de arquitetura de um conjunto de ferramentas
para o desenvolvimento de objetos em 3 dimensões. Há uma
preocupação bastente forte em definir um conjunto de interfaces
que possam ser utilizadas tanto por programadores como não programadores.
Para que "não programadores" tirem proveito da ferramenta, esta
apresenta recursos de manipulação direta das primitivas,
bem como interfaces amigáveis para definição de restrições.
O paradigma de programação visual apresenta ainda a vantagem
de facilitar a visualização de restrições complexas
entre primitivas.
Esta ferramenta já foi utilizada para criar ilustrações
matemáticas, construção de objetos de interface 3D,
construção de ferrametas interativas para operações
de modelagem mecânica e construção de ferrametas para
visualização científica.
As idéias básicas que caracterizam esta arquitertura são:
-
Cada primitiva deve possuir um conjunto de características que a
descrevam complentamente (slots),
-
Para que designers criem objetos complexos a partir de primitivas mais
simples ligadas através de restrições complexas, a
ferramenta possibilita a edição, através de uma interface
amigável, destas restrições
-
As primitivas "conhecem" os dispositivos de entrada, e são manipuladas
diretamente através da interação do usuário.
Qualquer manipulação deve preservar as restrições
já definidas.
Para garantir que a ferramenta seja facilmente extensível foi usado
um design orientado a objeto. Cada primitiva é representada por
uma classe, e cada instância da primitiva está associada à
uma instância desta classe. Cada classe contém membros chamados
"slots", que correspondem ao conjunto de atributos que caracterizam a primitiva.
É necessário agora definir mecanismos para estabelecer restrições
(quais "slots" estão relacionados e como), e mecanismos para garantir
que estas restrições sejam mantidas durante o processo de
interação.
Estes problemas foram solucionados definindo-se um conjunto comum de
métodos para as primitivas:
-
Inquiry - retorna o valor de um slot
-
Assignment - atribui valor a um slot
-
Establish - Estabelece uma situação inicial onde as
restrições são satisfeitas
-
Resolution - Este método resolve todos os slots da primitiva
(usando o método Inquire quando necessário), e atualiza
sua representação gráfica.
Estes métodos podem ser redefinidos pelo desenvolvedor para que
restrições novas sejam criadas.
Uma restrição não remove necessariamente todos
os graus de liberdade de um slot. Os graus de liberdade que sobram são
represendados por slots dinamicamente criados na primitiva. Por exemplo,
quando restringimos um ponto a um vetor, um slot T é
criado, e representa a posição paramétrica do ponto
no vetor. Neste caso o método Resolution primeiro deve resolver
o slot T, e só então passar o valor de T
e o vetor para o método Inquire para resolver o slot Pos
do ponto.
As promitivas básicas deste "toolkit" são:
Todas as outras formas devem ser criadas ligando-se estas primitivas através
de um conjunto de restrições.
A criação de novas estruturas é feita através
de Encapsulamento. Esta ferramenta define dois tipos de encapsulamento:
-
Encapsulamento Estrutural
Serve para ajudar o usuário a reproduzir uma estrutura de primitivas
ligadas através de um conjunto de restrições.
Similar ao encapsulamento estrutural mas permite que uma nova classe
seja associada à estrutura. Desta forma os métodos de interação
podem ser redefinidos e a nova classe se comporta como sendo uma nova primitiva
adicionada à ferramenta.
Estas duas formas de encapsulamento podem ser parametrizadas. Encapsulamentos
parametrizados permitem a criação da sua estrutura a partir
de informações fornecidas pelo usuário. Por exemplo,
o usuário fornece dois pontos para que seja criado um segmento de
reta entre eles.
De forma geral este trabalho é o início de pesquisa de
como criar ambientes de desenvolvimento de geometrias em três dimensões.
Os exemplos dados tratam de restrições e primitivas muito
simples, o que deixa a dúvida se realmente esta estrutura comporta
modelos complexos de uma forma "tratável". Com certeza, à
medida que se for criando classes mais complexas, problemas surgirão
e novas soluções ou paradigmas terão que ser incorporados
à ferramenta para que ela possa evoluir.
Bibliografia
[E. B.]
Eric A. Bier, Snap-Dragging in Three Dimensions, 1990, pp. 193 - 204.
[G.N. and D.O.] Gregory M. Nielson and Dan R. Olsen, Direct manipulation
techniques for 3D
objects using 2D locator devices, Proceedings of the 1986 workshop
on Interactive
3D graphics (October 23 - 24, 1986, Chapel Hill, NC USA) pp. 175 - 182.
[J.S.]
John M. Snyder. An Interactive Tool for Placing Curved Surfaces without
Interpenetration. Computer Graphics, 1995, pp. 209 - 218.
[K.S. and E.F.] Karan Singh e Eugene Fiume. Wires: A Geometric Deformation
Technique. Computer
Graphics, 1998, pp. 405 - 414.
[L.K.]
Lutz Kettner, Theoretical Foundations of 3D-Metaphors
[M.G. and A.W.] Michael Gleicher e Andrew Witkin. Through-the-Lens Camera
Control. Computer
Graphics, 1992, pp. 331 - 340.
[P..S. and R.C.] Paul S. Strauss e Rick Carey. An Object-Oriented 3D
Graphics Toolkit. 1992, pp.
341 - 347.
[R.B., T.B.,G.K. and G.F.] Ravin Balakrishnan, Thomas Baudel, Gordon
Kurtenbach e George
Fitzmaurice, The Rockin' Mouse: Integral 3D Manipulation on a Plane
[S. Z.]
Stevens, M.P., Zeleznik, R.C., Hughes, J.F. An Architecture for an Extensible
3D
Interface Toolkit. Proceedings of UIST '94, ACM SIGGRAPH, 1994.
[T.S. and S.P.] T. Sederberg and S. Parry. Free-Form deformation of
solid geometric models.
Computer Graphics, 20:151-160,1986.
[W.H, J.H. and H.K] W. Hsue, J. Hughes and H. Kaufman. Direct Manipulation
of
free-form deformations. Computer Graphics, 26(2): 177-184, 1992.
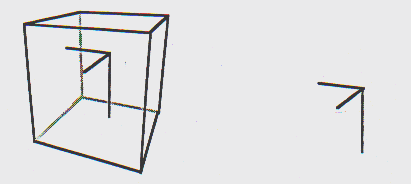
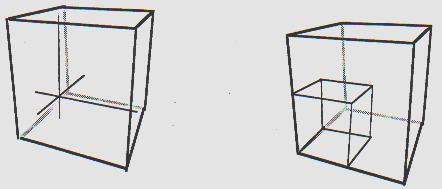





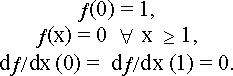

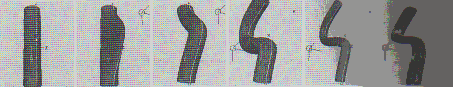
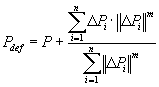 .
.