 (rib)
(rib)
 (rib)
(rib)
x'= x + dx (1)A translação é uma transformação de corpo rígido que move objetos sem deformá-los. Assim, cada ponto de um objeto é transladado da mesma quantia. Por exemplo, um segmento de reta que sofre translação, tem suas extremidades alteradas pelas relações (1), (2) e (3) e é, então, redesenhado a partir de suas novas extremidades. Um polígono, por sua vez, quando transladado, tem a posição de seus vértices alterada pelas relações (1), (2) e (3) e o novo conjunto de vértices originado é utilizado para recriar o polígono.
y'= y + dy (2)
z'= z + dz (3)
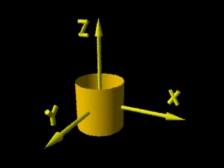
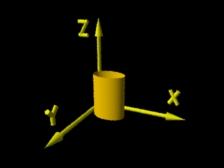
| Cilindro originalmente posicionado num sistema de coordenadas tridimensional xyz. |
 (rib)
(rib)
|
 (rib)
(rib)
|
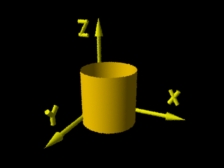
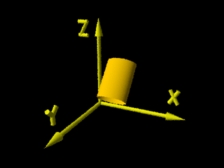
Cilindro após sofrer operação de translação. |
| Cilindro originalmente posicionado num sistema de coordenadas tridimensional xyz. |
 (rib)
(rib)
|
 (rib)
(rib)
|
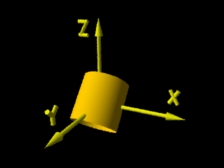
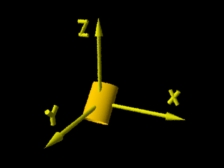
Cilindro após sofrer operação de rotação. |
x'= x.sxOs fatores sx, sy e sz podem assumir quaisquer valores positivos, sendo que para valores menores que 1, o tamanho do objeto é reduzido, para valores maiores que 1, o aumenta-se o tamanho do objeto e para valores igauis a 1, o tamanho original do objeto é mantido.
y'= y.sy (1)
z'= z.sz
| Cilindro originalmente posicionado num sistema de coordenadas tridimensional xyz. |
 (rib)
(rib)
|
 (rib)
(rib)
|
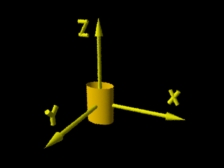
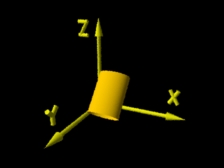
Cilindro após sofrer operação de escalamento. |

 (rib) Translação |
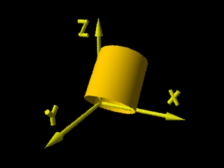 (rib) Translação e rotação |
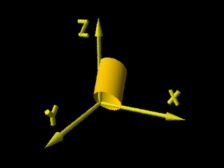 (rib) Translação, rotação e escalamento |
 (rib) Translação |
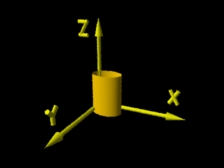 (rib) Translação e escalamento |
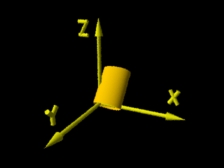 (rib) Translação, escalamento e rotação |
 (rib) Rotação |
 (rib) Rotação e translação |
 (rib) Rotação, translação e escalamento |
 (rib) Rotação |
 (rib) Rotação e escalamento |
 (rib) Rotação, escalamento e translação |
 (rib) Escalamento |
 (rib) Escalamento e translação |
 (rib) Escalamento, translação e rotação |
 (rib) Escalamento |
 (rib) Escalamento e rotação |
 (rib) Escalamento, rotação e translação |