Tese de Doutorado de Mercedes G. Márquez

Pré-alinhamento de Imagens de Profundidade via Malhas Simplificadas

(1) Imagem de Profundidade Vista 1

(2) Imagem de Profundidade Vista 2

(3) Pré-alinhamento das duas imagens

 

Introdução

O processo de Reconstrução 3D de objetos a partir de imagens de profundidade compreende três fases: aquisição, na qual a superfície do objeto é escaneada a partir de vários pontos de vista, gerando um conjunto de n imagens de profundidade. Registro, na qual uma transformação rígida (matriz de rotação e translação) deve ser estimada para colocar as imagens, par a par, em um único referencial. E integração, na qual redundâncias entre vistas registradas são tratadas para construir um modelo 3D completo único.

Na etapa de registro distinguem-se ainda duas etapas: pré-alinhamento e registro fino. Na primeira, uma aproximação inicial de registro é estimada através da extração de amostras nas duas imagens, que ocupem a mesma posição no espaço do objeto (pontos correspondentes) e o cálculo de uma transformação rígida T (matriz de rotação R e um vetor translação t) de forma que a distância quadrada entre os pares de pontos correspondentes, seja minimizada. Na segunda etapa, iterações são aplicadas sobre a transformação obtida para que os erros de alinhamento sejam minimizados.

As atuais técnicas de solução se diferenciam basicamente pela fonte de dados de onde os pares de correspondências são extraídos. Um primeiro grupo considera o conjunto completo de amostras originais e, um segundo, considera um subconjunto de amostras originais que possuem características especiais. As técnicas do primeiro grupo se tornam ineficientes ao propor um espaço de busca muito grande; e nas técnicas do segundo grupo, alguma informação importante para as correspondências pode ser descartada, ao restringir-se somente a um conjunto específico de dados (dependentes de certos tipos de geometria).

Neste trabalho propõe-se um algoritmo de registro que procura contornar estas limitações com base em duas inovações. O uso de uma malha triangular simplificada que preserve as características globais da forma original da imagem no lugar do conjunto completo de amostras originais e um novo descritor, denominado “triedro”, para buscar as correspondências, mais eficientemente, entre os espaços reduzidos das amostras. Diferentemente das propostas existentes, este descritor integra informações geométricas locais e globais das amostras, o que o leva a ser mais discriminante na busca. 

Hipótese

O sistema visual humano consegue fazer registro de objetos através da essência da sua forma. Adicionalmente, Belongie e Malik [1] afirmam que um objeto pode ser modelado como um possivelmente infinito conjunto de pontos, mas sua forma é essencialmente capturada por um subconjunto finito dos seus pontos. Portanto, no lugar de um conjunto de dados denso, pode-se usar um conjunto esparso de dados que aproxime a forma representada pelos dados originais. Assim, a hipótese deste trabalho é que, para realizar um pré-alinhamento, é suficiente considerar uma representação que, com poucas amostras, consiga exprimir a essência da forma geométrica pertencente à superfície do objeto.

  O Algoritmo

Nosso algoritmo de pré-alinhamento automático de duas imagens de profundidade é composto de três etapas: (A) Redução, (B) Construção de triedros e (C) Casamento, conforme mostramos na Figura 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

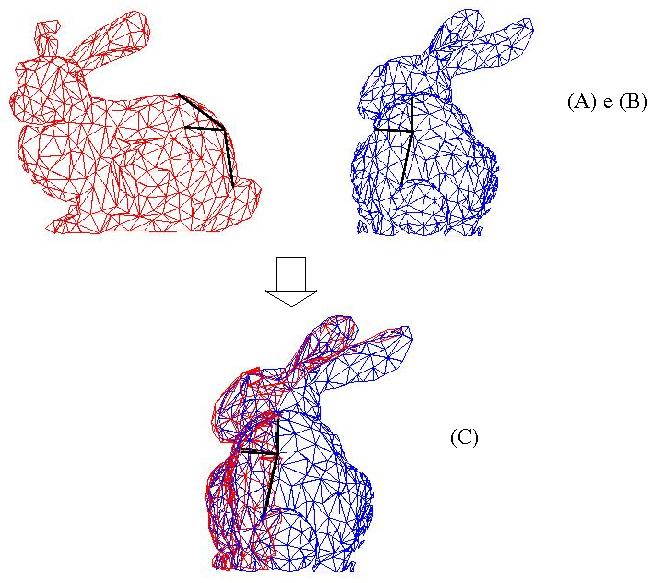
Figure 1: Fluxograma do Algoritmo

1) Redução

A etapa de redução é baseada na hipótese que uma representação simplificada da imagem de profundidade que retenha a essência da sua forma geométrica, é suficiente para obtermos um pré-alinhamento. Portanto dispensamos uma representação excessivamente detalhada e usamos somente uma versão simplificada. Propõe-se, então, uma malha simplificada (Figura 2(c)) da malha densa (Figura 2(b)), que foi construída pela interpolação das amostras da imagem de profundidade (Figura 2(a)).

 

(a) Imagem de profundidade

(b) Malha fina

(c) Malha simplificada

Figura 2. Redução de dados

 

Para obtermos a malha fina a partir da imagem de profundidade usou-se o procedimento simples sugerido em [2]. Para obtermos a malha simplificada é usado o algoritmo de simplificação QSLIM apresentado em [3] o qual usa o princípio de decimação por contração de arestas. Este princípio estabelece a eliminação de uma aresta e sua substituição por um ponto, à medida que se busca preservar maximamente a geometria da superfície, pela minimização dos erros introduzidos. Algumas adaptações precisaram ser feitas no algoritmo QSLIM para usá-lo no algoritmo proposto. No lugar do número de faces necessárias para controlar o nível de simplificação, usamos o parâmetro ε o qual depende do índice de suavidade estimado para a superfície e do número de amostras por área. Acredita-se que esses parâmetros influenciam fortemente o nível de resolução adequado para as malhas.

b) Construção de Triedros

A obtenção da transformação responsável pelo pré-alinhamento depende da determinação de um par de descritores correspondentes na região de sobreposição, portanto os descritores devem ser criteriosa e eficientemente extraídos a partir do conjunto de amostras da imagem. Propõe-se como descritor, um triedro espacial que consiste de três vetores linearmente independentes preferencialmente ortogonais, cuja origem e pontos extremos dos eixos, são vértices da malha triangular simplificada. A esse triedro será associada informação local (curvatura média) e, também, informação global (posição relativa de três vértices “suficientemente afastados” do vértice V na origem). O fato de se considerar uma região mais abrangente permite representar uma região com maiores aspectos da forma geométrica da superfície, ao invés de uma simples região local. Isto torna o descritor altamente discriminante na etapa de busca. Para determinar a distância di dos vértices do triedro até sua origem levou-se em conta dois requisitos conflitantes: maior abrangência e, por outro lado, a sua pertinência à região de sobreposição pois um descritor excessivamente grande pode não ficar inteiramente contido dentro desta região. Como a região de sobreposição é desconhecida, pensou-se em um valor conhecido relacionado com o tamanho do objeto, como a média M das dimensões da caixa limitante da malha que representa o objeto, onde M = (Dx + Dy + Dz )/3 com Dx denotando a largura, Dy a altura e Dz a profundidade da caixa limitante (Figura 3). Uma flexibilidade maior pode ser dada fazendo f1*M ≤ d ≤ f2*M , onde f1 < f2. Os valores f1 e f2 podem ser facilmente fornecidos pelo usuário como a menor e a maior estimativa da porcentagem, em pixels efetivos, que a região de sobreposição representa em relação à imagem de profundidade.

 

 

 

 

 

 

 

 

 

 

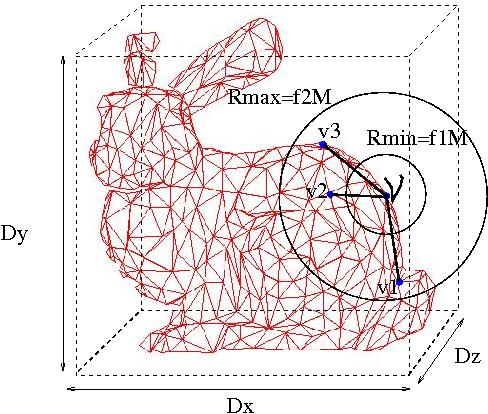
Figure 3: Construção de um Triedro

3) Casamento

Esta etapa é subdividida em duas sub-etapas: Procedimento de Busca por um Descritor-Alvo e Remoção de Correspondências Falsas.

Como procedimento de busca por um descritor-alvo, usou-se como base o princípio básico do algoritmo DARCES [4], o qual busca exaustivamente na imagem 2, três amostras extraídas da imagem 1. A proposta é percorrer vértices na malha M2 (associada à imagem 2) que sejam candidatos para se corresponderem com os vértices do triedro (descritor-referência) construído na malha M1 (associada à imagem 1). Seja Tk , um triedro definido no vértice V da malha M1, com vértices extremos vi , i = 1, 2, 3. Primeiro procura-se candidatos Cl em M2 para se corresponder com a origem V de Tk, pela comparação da curvatura média H2, a qual deve ser aproximadamente igual que a curvatura média H1 de V. O algoritmo de Rusinkiewicz [5] foi usado para cálculo robusto das curvaturas principais. Os potenciais correspondentes c1l e c2l de v1 e v2, respectivamente, são obtidos na mesma forma como no algoritmo DARCES, com uma restrição adicional: possuir similar curvatura média. Isto é, a região de busca dos pontos c1l é reduzida à superfície da esfera com raio V − v1 e centro em Cl e a região de busca dos pontos c2l é restrita à interseção das esferas de raios V − v2 e v1−v2, com centros em Cl e c1l, respectivamente [4]. Finalmente, uma busca dos candidatos c3l que correspondem a v3, poderia ser restrita à interseção de três esferas, porém uma região mais reduzida é obtida ao se seguir o seguinte procedimento: calcula-se a distância ponto-plano d de v3 até o plano P, formado pelos vetores Vv1 e Vv2, e calcula-se também as coordenadas baricêntricas, da projeção ortogonal x2 do vértice v3 sobre o plano P em relação ao triângulo Vv1v2. Logo, os pontos candidatos c3l estarão em um raio pequeno em volta do ponto p, sendo p = x2 + n2d, onde x2 é a posição correspondente a x1 no triângulo Cl c1lc2l e n2 é o vetor normal do plano gerado pelos vetores Clc1l e Clc2l (Figura 4).

 

 

 

 

 

 

 

 

 

Figure 4: Procura do quarto ponto

O casamento dos triedros reduz drasticamente o número de possíveis correspondências, porém ainda se tem um conjunto considerável de remanescentes. A transformação candidata Tk (Rk,tk) é determinada a partir de um par de triedros correspondentes T1 e T2 constituídos pelos vértices (V, v1 , v2 , v3 ) e (C, c1 , c2 , c3 ) respectivamente. Para remover falsas correspondências, cada transformação candidata Tk passa por uma avaliação de ajuste global através da contagem de vértices na malha transformada M1 , que alinharam suficientemente bem com vértices na malha M2 (ou seja sua distância até a malha M2 é menor que um limiar pré-definido). Dentre todas as transformações candidatas, escolhe-se aquela que teve o maior número de alinhamentos, baseado no fato que a transformação que registra a região de sobreposição de ambas imagens deve ter a maior quantidade de vértices alinhados.

Implementação

  A implementação do algoritmo proposto pode ser obtida clicando aqui. Os códigos foram desenvolvidos usando linguagem C e a biblioteca gráfica OpenGL. As imagens de entrada podem ser obtidas em [6],[7] ou [8].

This program is free software: you can redistribute it and/or modify  it under the terms
of the GNU General Public License as published by the Free Software Foundation, either 
version 3 of the License, or (at your option) any later version. This program is 
distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the 
implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
General Public License for more details. You should have received a copy of the GNU 
General Public License along with this program. If not, see http://www.gnu.org/licenses/.

  Publicações

1) Tese de Doutorado

·         Pré-alinhamento de Imagens de Profundidade via Malhas Simplificadas [pdf]
Autora: Mercedes Rocío Gonzales Márquez

2) Artigos Publicados

·    A non-self-intersection Douglas-Peucker Algorithm [pdf]

      Autores: Mercedes Rocío Gonzales Márquez e Wu Shin-Ting
Publicado em Proceedings of the 16th Brazilian Symposium on Computer Graphics and Image Processing

 

·         The Douglas-Peucker Algorithm: Sufficiency Conditions for Non-Self-Intersections [pdf]
Authors: Wu Shin-Ting, Adler Cardoso Gomes da Silva, e Mercedes Rocío Gonzales Márquez
Publicado no Journal of the Brazilian Computer Society

 

·         Using simplified meshes for crude registration of two partially overlapping range images[pdf]
Autores: Mercedes Rocío Gonzales Márquez e Wu Shin-Ting
Publicado em Short Communications Proceedings of the 15th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision'2007

 

·         An automatic crude registration of two partially overlapping range images [pdf]
Autores: Mercedes Rocío Gonzales Márquez e Wu Shin-Ting
Publicado em Proceedings of the 21th Brazilian Symposium on Computer Graphics and Image Processing

 

 ·         Crude registration of range images through matching of their simplified meshes [pdf]
Autores: Mercedes Rocío Gonzales Márquez e Wu Shin-Ting
Aceito para publicação em Proceedings of the Eleventh IASTED International Conference on Computer Graphics and Imaging – CGIM 2010

 

Referências

 

[1] S.Belongie and J.Malik. Shape matching and object recognition using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24:509–522, 2002.

[2] G. Turk and M. Levoy. Zippered polygon meshes from range images. In Computer Graphics Proceedings, pp. 311-318. Florida, 1994. Siggraph 94.

[3] Michael Garland. Simplification Using Quadric Error Metrics. PhD thesis, School of Computer Science Carnegie Mellon University, New York, USA, 1999.

[4] Chu-Song Chen, Yi-Ping Hung, and Jen-Bo Cheng. RANSAC-based DARCES: A new approach to fast automatic registration of partially overlapping range images. IEEE Transactions on Pattern Analysis and Machine Intelligence, pages 1229–1234, 1999.

[5] Szymon Rusinkiewicz. Estimating curvatures and their derivatives on triangle meshes. In 3DPVT’04: Proceedings of the 3D Data Processing, Visualization, and Transmission, 2nd International Symposium on (3DPVT’04), pages 486–493, Washington,DC,USA, 2004.

[6] Range images (Universidade Ohio State) . http://sampl.ece.ohio-state.edu/data/3DDB/RID/minolta/

[7] Range images (Universidade de Standford). http://www-graphics.stanford.edu/data/

[8] Range images (Universidade de Sttutgart). http://range.informatik.uni-stuttgart.de/htdocs/html/