Lista 3 - Compiladores
|
|
|
|
|
|
|
|
|
|
Obs.: Soluções alternativas para as correções dos problemas dos exercícios foram consideradas durante a correção.
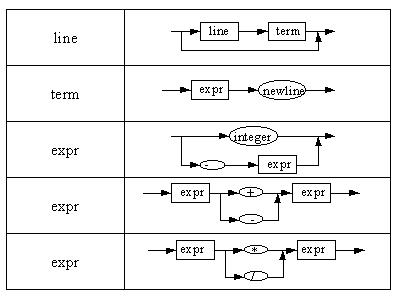
Descreva em termos de grafos sintáticos a gramática expressa a seguir em notação BNF:
<line> ::= [<line> <term>]
<term> ::= <expr> newline
<expr> ::= integer | -<expr>
<expr> ::= <expr> (+|-) <expr>
<expr> ::= <expr> (*|/) <expr>

Desenvolva o autômato finito determinístico com mínimo número de estados para reconhecer sentenças descritas pela expressão regular ( x x ) * ( y | z) z* [Exercício 3.2 da apostila].
I) Criar o Autômato Não Determinístico:
R1 = x
R2 = R1.R1
R3 = R2*
R4 = y
R5 = z
R6 = R4|R5
R7 = R3.R6
R8 = z
R9 = R8*
R = R7.R9
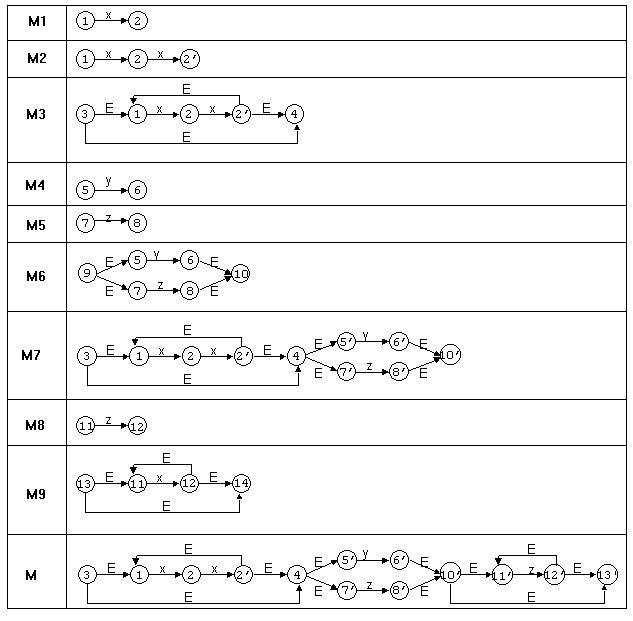
Renomeando os estados, tem-se o seguinte autômato não determinístico:

II) Transformar o
Autômato Não Determinístico em Autômato Determinístico:
|
|
|
| T0 = {0} | S0 = {0, 1, 4, 5, 7} |
| T1 = {2} | S1 = {2} |
| T2 = {6} | S2 = {6, 9, 10, 12} (Estado Final) |
| T3 = {8} | S3 = {8, 9, 10, 12} (Estado Final) |
| T4 = {3} | S4 = {3, 1, 4, 5, 7} |
| T5 = {11} | S5 = {10, 11, 12} (Estado Final) |
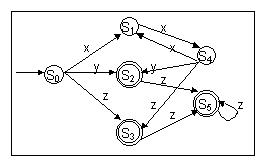
III) Minimizar o número de estados:
II0 = {{S0, S1, S4},
{ S2, S3, S5}}
G1
G2
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II1 = {{S0, S4}, {S1},
{ S2, S3, S5}}
G3 G4
G2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
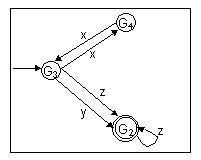
II2 = {{S0, S4}, {S1},
{ S2, S3, S5}}
G3 G4
G2
Estenda o programa da calculadora (lex/yacc) apresentado em aula de forma a agregar a seguinte seqüência de funcionalidades:
a. notação em ponto flutuante (exemplo: 2.4) e de engenharia (exemplo: 1.45E-3);
b. operador ** (exponenciação);
c. algumas funções "científicas" (trigonométricas e logarítmicas, por exemplo);
d. uso do token = para terminar uma expressão; assim, é possível ter seqüências de entrada com mais de uma linha;
e. especificação de um nome de arquivo em disco que contenha a seqüência de entrada a ser lida. O nome do arquivo é passado como parâmetro do programa (dica: redirecione yyin).
/* lex */
%{
#include "y.tab.h"
extern int lineno;
%}
integer [0-9]+
real [0-9]*"."[0-9]*
bigreal {real}[E|e][-|+]?{integer}
nl
\n
equal
=
power
"**"
%%
[ \t]+ ;
{integer}
{sscanf(yytext, "%d", &yylval.integer); return INTEGER;}
{real}
{sscanf(yytext, "%f", &yylval.real); return REAL;}
{bigreal}
{sscanf(yytext, "%lf", &yylval.real); return BIGREAL;}
{nl}
{lineno++;} /* no return ! */
{equal}
{return '=';}
{power}
{yylval.power = yytext; return POWER;}
sin
{return SIN;}
cos
{return COS;}
tan
{return TAN;}
.
{return yytext[0];}
%%
_____________________________________
/* yacc */
/* Gramatica: {Vt,
Vn, P, S}
* Vt = {INTEGER,
REAL, +, -, *, /, (, ), **, sin, cos, tan, =}
* Vn = {line,
term, expr}
* P = {
*
line -> epsilon
*
line -> term
*
term -> newline
*
term -> expr newline
*
expr -> intnumer
*
expr -> expr + expr
*
expr -> expr - expr
*
expr -> expr * expr
*
expr -> expr / expr
*
expr -> expr ** expr
*
expr -> sin(expr)
*
expr -> cos(expr)
*
expr -> tan(expr)
*
expr -> (expr)
*
expr -> -expr
*
}
* S = line
*/
%{
#include <stdio.h>
#include <math.h>
extern FILE* yyin;
%}
%union
{
double
bigreal;
float
real;
int
integer;
char*
power;
}
%token <integer>
INTEGER
%token <bigreal>
BIGREAL
%token <real>
REAL
%token <power>
POWER
%token SIN COS TAN
%type <bigreal> expr;
%left '+' '-'
%left '*' '/'
%left POWER
/* power */
%nonassoc UMINUS
%%
lines:/* nothing
*/
| lines line
;
line: '='
| expr '=' {printf("%lf\n", $1);}
| error '=' {yyerror;}
;
expr: BIGREAL
| INTEGER {$$ = $1;}
| REAL {$$ = $1;}
| SIN '(' expr ')' {$$ = sin($3);}
| COS '(' expr ')' {$$ = cos($3);}
| TAN '(' expr ')' {$$ = tan($3);}
| expr '+' expr {$$ = $1 + $3;}
| expr '-' expr {$$ = $1 - $3;}
| expr '*' expr {$$ = $1 * $3;}
| expr '/' expr {
if($3) $$ = $1 / $3;
else
{
printf("divide by zero");
yyerror;
}
}
| '(' expr ')' {$$ = $2;}
| expr POWER expr %prec POWER {$$ = pow($1, $3);}
| '-' expr %prec UMINUS {$$ = - $2;}
;
%%
int lineno = 0;
main(int argc, char*
argv[])
{
if(argc
== 2)
{
yyin = fopen(argv[1], "r");
if(yyin == NULL)
{
printf("%s: no such file\n", argv[1]);
exit(1);
}
}
yyparse();
fclose(yyin);
}
yyerror(s)
char *s;
{
printf("calc:
%s\n", s);
printf("line
%d\n", lineno);
}
Considere a compilação da seguinte especificação yacc:
%token CMD
COND ELSE IF
%%
stmt
: CMD
| ifstmt
;
ifstmt
: IF '(' COND ')' stmt
| IF '(' COND ')' stmt ELSE stmt
;
Observe a mensagem de erro produzida pelo yacc e explique o seu significado. Essa mensagem indica um erro fatal?
O compilador bison apresenta a seguinte mensagem: "gram.y contains 1 shift/reduce conflict."
Essa mensagem significa que uma das regras da gramática não especifica completamente o modo com o qual todas as entradas complexas devem ser estruturadas. Isto quer dizer que a gramática possui uma ambiguidade, isto é, existe mais de uma maneira de se produzir um parser para essa gramática.
Essa mensagem não indica um erro fatal, pois existe uma regra clara que o yacc utiliza para tratar o conflito. Veja em http://uw7doc.sco.com/SDK_tools/_Ambiguity_and_Conflicts.html mais detalhes sobre esse tipo de conflito e como o yacc o resolve.
5. Dada a expressão x = (a+b+c)*(b+c)+d,
a. reescreva-a usando código intermediário de três endereços;a)
b. reescreva-a usando notação pósfixa;
c. a expressão é passível de otimização? Se sim, indique as possibilidades.
b)
ab+c+bc+*d+
ou abc++bc+*d+
c)
Sim. Através
do uso da propriedade algébrica de comutatividade:
_t1 = b + c
_t2 = _t1 + a
_t3 = _t2 * _t1
x = _t3 + d