


Next: Sobre este documento...
Universidade Estadual de Campinas
FACULDADE DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO
IA725 -- 1
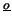 Semestre de 2003 Semestre de 2003
|
IA725 - Computação Gráfica
Prova 1
27/03/2003 - 8:00 às 9:50h
Profa. Wu, Shin - Ting
- Questão 1:
- Dada a equação
- (0.5 pt) A qual tipo de seção cônica corresponde a equação (hipérbole, parábola ou elipse)?
- (0.5 pt) Qual é a matriz que transforma os eixos do sistema
de referência no qual está definido a figura acima para as suas
direções principais da seção cônica?
- (1.0 pt) Seja
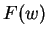 ,
, 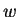 em radianos, a transformada de Fourier
de
em radianos, a transformada de Fourier
de 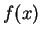 . Mostre que
. Mostre que
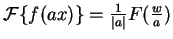 ,
,
 .
.
- (0.5 pt) Se aumentarmos a escala de uma função no domínio espacial, o que
acontece com a escala no domínio de frequências? (Dica: Analisar a igualdade
no item anterior).
- Questão 2:
- Dadas as funções de base
- de Hermite cúbicas
- de Bernstein
- de Base
e
- (0.5 pt) Qual é a matriz de conversão de grandezas geométricas
que definem uma curva de Hermite em grandezas que definem uma curva de
Bézier?
- (1.5 pt) Esboce os gráficos das funções
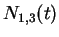 ,
,
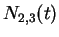 ,
, 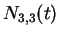 ,
,  e
e 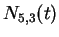 para um vetor
de nós
para um vetor
de nós
![$[0~0~0~1~1~3~3~3]$](img25.gif) .
.
- (0.5 pt) Como seriam as expressões das funções
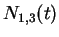 ,
,
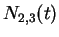 ,
, 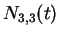 ,
,  e
e 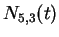 para as curvas
de B-splines racionais com os seguintes pesos
para as curvas
de B-splines racionais com os seguintes pesos ![$[1~1~0.5~1~1]$](img26.gif) ?
?
- Questão 3:
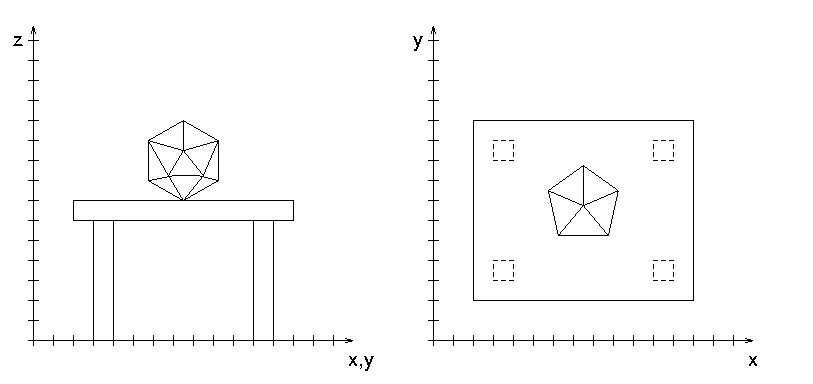
- Para modelar uma cena contendo uma bola de raio de 2
unidades sobre uma mesa, foram utilizados os modelos abaixo
As coordenadas dos 12 vértices do modelo da bola centrado na origem são
onde
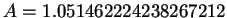 e
e
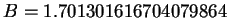 .
.
- (1.0 pt) Utilize a codificação vértice-face para descrever a
geometria do tampo da mesa e uma das pernas.
Explique sucintamente a sintaxe
que você adotou. (Dica: não se esqueça da
coerência nas orientações das faces e das quantidades
de vértices e faces!)
- (0.5 pt) Como poderemos visualizar a bola sem as pontas?
- (0.5 pt) Mostre que
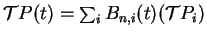 .
para as transformações afins.
.
para as transformações afins.
- (0.5 pt) Determine a matriz de rotação da mesa em torno do centro da mesa
por um ângulo de
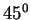 no sentido anti-horário.
no sentido anti-horário.
- (1.0 pt) Derive a matriz de rotação de um ponto
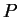 em torno de um eixo
unitário
em torno de um eixo
unitário
![$[n_x ~n_y ~n_z]$](img34.gif) que passa pela origem por um ângulo
que passa pela origem por um ângulo
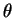 .
.
- Questão 4:
- Dados os parâmetros de uma câmera:
- a posição:
![$P=[3.0~4.0~-4.0~1]^t$](img36.gif)
- centro de interesse:
![$C= [0~0~0~1]^t$](img37.gif) (o eixo focal é a
reta que passa pela câmera e o seu centro de interesse)
(o eixo focal é a
reta que passa pela câmera e o seu centro de interesse)
- orientaçõ:
![$VUP = [0~-1.0~0~0]^t$](img38.gif)
- (1.0 pt) Determine a transformação do sistema no qual está definida a
câmera para um novo sistema
em que a câmera fique na origem, o vetor
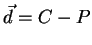 coincida com o eixo
coincida com o eixo 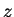 e que o vetor
e que o vetor  fique no plano
fique no plano 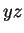 .
.
- (0.5 pt) Qual é a distância do plano de projação em relação à posição da
câmera?



Next: Sobre este documento...
Wu Shin Ting
2003-03-27

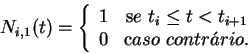
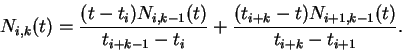
![\begin{displaymath}
\left[\begin{array}{c}
-A \\
0 \\
B
\end{array}\right],~\l...
...ht],~\left[\begin{array}{c}
0 \\
B \\
-A
\end{array}\right],
\end{displaymath}](img27.gif)
![\begin{displaymath}
\left[\begin{array}{c}
0 \\
-B \\
A
\end{array}\right],~\l...
...t],~\left[\begin{array}{c}
-B \\
-A \\
0
\end{array}\right],
\end{displaymath}](img28.gif)
![]() e
e
![]() .
.