Algoritmo do Corte Mediano

Indicamos por K o número de níveis de quantização desejado. Tomamos um paralelepípedo

                              V={[r₀,r₁]x[g₀,g₁]x[b₀,b₁]}

De volume mínimo que contém todas as cores no gamute da imagem a ser quantizada. Em seguida, tomamos a componente do espaço de cor em cuja direção o paralelepípedo V possui a aresta de maior comprimento. Vamos supor que essa é a componente verde g. Fazemos então uma ordenação das cores no gamute da imagem pela componente g, e calculamos a mediana m_g do conjunto de cores com base nessa ordenação. Dividimos assim a região V em duas sub-regiões:

                              V₁ = { (r,g,b) Î C;g £ m_g },

e                            V₂ = { (r,g,b) Î C;g ³ m_g }.

Aplicamos então o mesmo método de subdivisão a cada uma das regiões V₁ e V₂. Continuamos o processo de subdivisão, recursivamente, até que uma das duas condições seguintes sejam satisfeitas: as duas sub-regiões V₁ e V₂ obtidas não contêm cores no gamute da imagem, ou o número desejado, K, de células de quantização já foi obtido.

Após a subdivisão do espaço de cor no número de células desejado, determinamos o nível de quantização de cada célula. Para se obter o valor de quantização de um pixel da imagem, devemos localizar a célula que contém a cor desse pixel, e fazer a quantização para o nível correspondente a essa célula. A implementação do algoritmo pode ser feita de modo eficiente utilizando-se uma estrutura de dados espaciais adequada no processo de subdivisão recursiva do espaço de cor.

Vejamos um exemplo para o caso de um espaço de cor bidimensional.

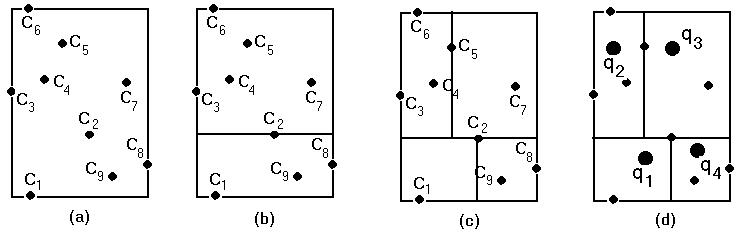
Exemplo 1- Considere um conjunto bidimensional de 9 cores distintas, mostrado na figura 2(a), cujas freqüências são dadas pela tabela à esquerda, abaixo.

A direção mais longa do retângulo de cores é a vertical. Ordenando as cores pela ordenada y, obtemos a tabela à direita acima.

Figura 2- (a) (b) e (c) – subdivisão recursiva pelo corte mediano; (d) Níveis de quantização

É imediato verificar que a mediana do conjunto está na posição 7,5, e portanto, é dada pela média das cores nas posições 7 e 8. Como essas posições são ocupadas pela cor C₂, concluímos que a mediana é C₂. A Figura 2(b), mostra a subdivisão. A aresta mais longa de cada um desses retângulos é a horizontal. Ordenando as cores pela componente horizontal x, obtemos as duas tabelas de freqüência abaixo:

 No primeiro caso, a mediana é a cor C₂, e no segundo caso, a mediana é a cor C₅. As subdivisões correspondentes no retângulo de cor aparecem na Figura 2(c).

Após determinadas as quatro células de quantização, o nível de quantização em cada célula é calculado tomando a média das cores do gamute em cada célula. As cores que estão no bordo da célula devem ser quantizadas para o nível de quantização mais próximo. A Figura 2(d) mostra os quatro níveis de quantização associados a cada célula de quantização. A função de quantização q é dada pela tabela abaixo: