A HYBRID CHC GENETIC
ALGORITHM FOR MACRO CELL GLOBAL ROUTING
G.Andal Jayalakshmi*,
S.Sowmyalakshmi* and R.Rajaram**
*Department of Computer
Science and Engineering
** Department of Information
Technology
Thiagarajar College of
Engineering, Madurai –625015, Tamilnadu, India
ABSTRACT
Global routing for VLSI circuits has received wide attraction. In this paper we have presented a Hybrid CHC (HCHC) genetic algorithm for global routing. The hybridization is required for initializing population with feasible solutions. The CHC algorithm is used for evolution. The algorithm was tested for standard test problems and compared with a simple GA. The CHC identified trees very nearer to the optimum and performed better than the simple GA.
1. INTRODUCTION
One of the most important VLSI Design Approaches is the Macro Cell design. Macro cells are large, irregularly sized parameterized circuit modules that are generated by a silicon compiler as per a designer’s selected parameters. Usually the physical design process for macro cells is divided into Floor Planning / Placement, Global Routing and Detailed Routing. Floor Planning / Placement constructs a layout indicating the position of the macro cells. The placement is then followed by routing, which is the process of determining the connection pattern for each net to minimize the overall routing area. Both the placement and routing problems are known to be NP-complete[1]. Thus it is impossible to find optimal solutions in practice and various heuristics are used to obtain a near optimal solution. There has been a lot of work on optimization for routing, including Simulated Annealing algorithms and Genetic Algorithms (GA) for both placement [1, 2, 3] and routing [4].
Usually the physical design process is divided in to the following steps: Floor planning / Placement, Pin assignment, Global routing and Detailed routing. In Floor planning the dimensions and locations of the macro cells are determined. In the Pin assignment step, the locations of pins on the macro boundaries are determined. Global routing assigns the routing regions for connecting the pins of the same net. Detailed routing generates the actual geometric layout for the interconnections.
In this paper we have implemented a hybrid CHC genetic algorithm for global routing. The algorithm is tested for three standard test problems
2. PROBLEM DEFINITION
The Minimum Rectilinear Steiner Tree (MRST) problem arises in global routing and wiring estimation where we seek low-cost topologies to connect the pins of signal nets [5]. Research on the MRST problem has been guided by several fundamental results. Hanan[6] has shown that there always exists an MRST with Steiner points chosen from the intersections of all the horizontal and vertical lines passing through all the points in P and this result was generalized by Snyder[7] to all higher dimensions. However a result by Garey and Johnson[8] establishes that despite this restriction on the solution space, the MRST problem remains NP-complete, this has given rise to numerous heuristics as surveyed by Hwang, Richards and Winter [9].
The MRST problem can be defined as below: Given n points in the Euclidean plane, we seek a tree that connects them all. If the edges in this tree are to be selected from all possible edges, that is from the complete graph on the points, we have the familiar problem of finding a spanning tree in an undirected graph. If the edges of the tree must be horizontal and vertical, the additional points where the edges meet are called Steiner points, and the resulting tree is a rectilinear Steiner tree. A shortest such tree on a set of given points is a Minimal Rectilinear Steiner Tree(MRST)[10].
3. THE GLOBAL ROUTER
ALGORITHM
Before the global routing process begins a routing graph is extracted from the given placement. Routing is done based on this graph. Computing a global route for a net corresponds to finding a corresponding path in the routing graph. Each edge represents a routing channel and the vertex is the intersection of the two channels. First the vertices that represent the terminal of the net are added to the routing graph. Then the shortest route for the net is found which is nothing but the Steiner Problem in Graphs. Then the global routing problem is formulated as finding the Steiner Minimal Tree on the routing graph.
The algorithm is divided into two phases:
Phase 1:
The Steiner tree algorithm we developed is based on the
shortest path heuristic. We developed a simple genetic algorithm for the
construction of a minimum spanning tree, which is used in the generation of the
Steiner minimum tree.
The algorithm for SPANNING_TREE() is given below:
SPANNING_TREE(
)
Begin
Initialize parameters : generation count , crossover and mutation
probabilities
Initialize parent population randomly
Apply repair heuristics to the parent population /* Repair
heuristics are
To test cycle and self loops*/
While ( termination condition not
reached)
Begin
Select parents based on the
total length of the Spanning tree
Apply crossover and mutation
/* Single Point Crossover and Exchange
Mutation*/
Evolve new population
Replace previous population
by new population
End
End
The Cycle and Self loop tester are implemented to remove cycles and self loops from the population and hence make the population a set of feasible solutions.
Phase 2:
The Steiner points are restricted to the Hanan grid[6], formed by the intersections of vertical and horizontal lines passing through the initial demand points. There are various heuristics available to construct a MRST, and most of them use MST as a starting point.
The I-Steiner algorithm[11] constructs the MRST by evaluating all possible Steiner points for their impact on MST cost. The algorithm operates on a series of passes, in each pass the single Steiner point which provides the greatest improvement in spanning tree cost is selected and added to the set of demand points. Points are added until no further improvement can be obtained. In experiments with random point sets, this algorithm obtains nearly 11% improvements over MST on an average.
The heuristics we have used here for the construction of MRST is the “BOI” or “edge-removal technique” of Borah, Owen and Irwin [12]. In this approach, an edge and a vertex pair that are close to each other in an MST are determined. A cycle is introduced, if the vertex is connected to some location on the edge; this cycle can be eliminated by removing a second edge along the cycle. The BOI approach determines a set of these pairings along with edges that are to be removed. The edges are removed and new connections are inserted until no improvements can be obtained. The approach has low complexity with performance comparable to that of I-Steiner.
The algorithm is given below:
STEINER_TREE( )
Begin
Build the routing graph G
For (each Net)
Begin
Initialize weights
for edges.
Find the minimum
cost spanning tree T.
For each (vertex,
edge) pair of the spanning tree
Begin
Find the optimum Steiner point to connect
this edge to the vertex (at a suitable point)
Find the longest edge on the generated
cycle
Compute the cost
of the modified tree, and store the pair in a list, if the cost is less than
the MST
End
While the list is not empty
Begin
Remove the pair from the list which
results in lowest cost
Re compute the longest edge on the cycle
and the cost of the tree
If the edges to be replaced are in the
tree and the cost is less modify the
tree
End
End
End
4. THE HYBRID CHC GENETIC ALGORITHM
A Genetic Algorithm is an intelligent optimization technique used to solve many complex optimization problems. A simple GA evolves a solution from an initial population of random solutions using crossover and mutation. An SGA often fails to produce an optimal solution within an acceptable time because of the random initialization. Hence hybridization techniques are used to initialize the population to reduce the search space. A hybrid GA combines techniques particular to a problem with the simple GA. The simplest hybrid GA applies problem-specific information to operate on fairly good organisms and then operates as conventional GA. In this paper we present a Hybrid CHC Genetic Algorithm for the global routing of Macro cell layouts. A CHC genetic algorithm uses intelligent reproduction techniques and techniques to come out of local optima.
CHC, which is a non-traditional genetic algorithm is used in this paper, it
differs from a classic GA as follows
- For a population
of N, it guarantees that the best individuals found so far shall always
survive by putting the children and parents together leading to 2N
individuals and selecting the best N individuals for further processing.
- To avoid premature
convergence, two similar individuals separated by a small Hamming distance
are not allowed to mate.
- Mutation isn't
needed during normal processing.
- An external
mutation operator re-initializes the population when the population has
converged or search has stagnated.
The pseudo-code for the Hybrid CHC genetic algorithm is shown below:
HCHC( )
Begin
Set the generation count c = 1
Set threshold
value
Initialize and
evaluate parent population P(t)
While
(Termination Condition is not reached) do
c = c + 1
Apply selection
Perform crossover on selected
individuals to get Offspring C(t)
Evaluate Offspring C(t)
Select new parent population from
previous parent population P(t-1) and
the new child population
C(t) using Elitism
If P(t) is equal to P(t-1) then decrease the
threshold value
If Convergence occurs
Reinitialize population by
external mutation.
End
End
To guarantee that the best individuals found so far will always survive, elitist selection makes the newly created children compete with the members of the parent population for survival by merging and ranking them according to their fitness values. If the GA's population is N, 2N candidates will compete for the N positions in the next generation. A mechanism is used to slow premature convergence, It checks the Hamming distance between two potential parents before their crossover. If half of the Hamming distance does not exceed a convergence threshold, the two individuals are not allowed to mate. Whenever no children are accepted into the next generation either because no potential mates were mated or because none of the children were better than the worst member of the parent population, the convergence threshold is decreased. Premature convergence happens when the threshold drops to zero. An outside mutation is used to re-initialize the population by keeping the best individual found so far and initializing the others randomly. The convergence threshold is also reset. The CHC genetic algorithm generally does well with small population sizes. This is because CHC is able to maintain population diversity in a small population size without sacrificing implicit parallelism by combining a highly disruptive crossover operator with a conservative selection procedure that preserves any progress ever made.
5. SOLUTION ENCODING
Most GAs use binary strings for encoding due to simple implementation and simple crossover and mutation operators. However integer encoding is also used, especially in complex problems. Our Encoding consists of an array of integers that represent the edges of the graph in the case of a Minimum Spanning Tree and the edges of a Steiner graph in the case of a Steiner Minimal Tree.
6. CHC GENETIC OPERATORS
Reproduction Operator
The crossover operator is used to generate offspring from the parents chosen by the selection schemes. We use Uniform crossover. It is implemented along with the repair algorithm. The repair algorithm act on the infeasible chromosomes and convert them to feasible ones.
Mutation
We use Random mutation, which randomly changes a gene in the chromosome In CHC genetic algorithm when premature convergence occur we reinitialize the whole population by means of random mutation.
7. IMPLEMENTATION AND RESULTS
The HCHC algorithm is implemented and three standard test problems B1,B3 and B9 from the problem sets of J.E.Beasley [13] are tested. The results are comparable and are tabulated in this section. A simple GA with one point crossover and exchange mutation is also implemented and the results are compared with the HCHC algorithm. In HCHC, Uniform crossover and Random mutation are used for reproduction. The probabilities of crossover and mutation are set at 0.5 and 0.03 respectively for both SGA and HCHC. The convergence threshold is set to 7.5. The best results out of 10 independent runs for the test problems are given below:
Test Problem : B1
Nodes : 50 Edges : 63 Optimum : 82
Population Size for SGA : 110
Population Size for HCHC: 90
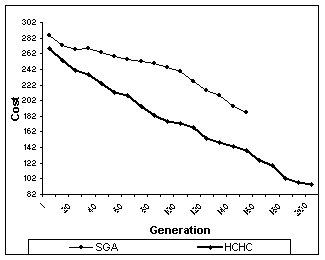
Graph 1: Comparison of cost reduction in SGA and HCHC algorithms for B1
Test Problem : B3
Nodes:50 Edges:63 Optimum : 138
Population Size for SGA : 110
Population Size for HCHC: 90
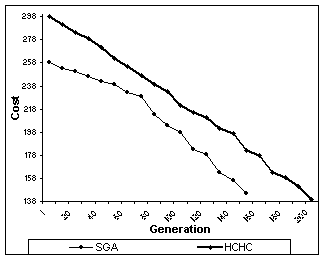
Graph 2: Comparison of cost reduction in SGA and HCHC algorithms for B3
Test Problem : B9
Nodes:75 Edges:94 Optimum : 220
Population Size for SGA : 110
Population Size for HCHC: 90
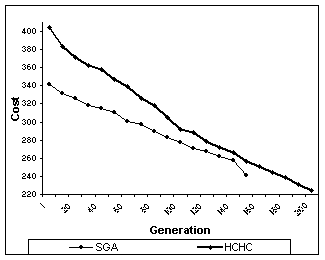
Graph 3: Comparison of cost reduction in SGA and HCHC algorithms for B9
CONCLUSION
In this paper we have presented a HCHC genetic algorithm for macro-cell global routing. The HCHC algorithm shows much better performance over SGA, and generates comparable results for the Beasley’s problem set. We further propose to improve the implementation for higher number of nodes and compare the results with the other existing algorithms.
REFERENCES
1. K.Shahookar and P,Mazumder, VLSI cell placement techniques, in ACM Computing surveys, vol 23, pp.143-220, Jun 1991
2. J.P.Cohoon and W.D.Paris, Genetic placement in proceedings of the IEEE International conference on Computer aided design, pp.422-425, 1986
3. R.M.Kling, Placement by simulated evolution master’s thesis in coordinated science lab, college of Engg., Univ of Illinois at Urbana Campaign, 1987
4. H.Esbensen, A macro cell global router based on two genetic algorithms, in Proc of European Design Automation Conf, Euro-DAC, pp 428-433, Grenoble, France Sep 1994.
5. B.T.Preas and M.J.Lorenzetti, Physical design automation of vlsi systems, Benjamin/Cummings, Menlo Park, CA, 1988
6. M.Hanan, On Steiner’s problem with rectilinear distance, SIAM Journal, Applied mathematics, 14(1966) pp.255-265
7. T.I.Snyder, On the exact location od stiner points in general dimension, SIAM J, Comp, 21(1992) pp.163-180
8. M.Garey and D.S.Johnson, The Rectilinear stiner problem is NP-Complete, SIAM J, Applied mathematics, 32(1977) pp.826-834
9. F.K.Hwang, D.S.Richards and P.Winter, The Steiner tree problem, North Holland, 1992
10. Bryant A.Julstrom, Seeding the population: Improved performance in a genetic algorithm for the rectilinear Steiner problem, ACM 089791 – 647 – 6 /94/0003, 1994
11. A.B.Kahng and G.Robins, A new class of iterative Steiner tree heuristics with good performance , IEEE Trans on Computer Aided design of Integrated circuits and systems, 11(7), 1992, pp.893-902
12. M.Borah, R.M.Owens and M.J.Irwin, An edge based heuristic for Steiner routing, IEEE trans on Computer Aided design of Integrated circuits and systems, 13(12), Dec 1994, pp.1563-1568
13. J.E.Beasley, An SST-based algorithm for the Steiner problem in graphs, Netwoks, 19, 1989, pp.1-16.