 EA-869 - Dúvidas Frequentes
EA-869 - Dúvidas Frequentes
EA-869 - Dúvidas Frequentes
Capítulo VIII (01.6.98), 01/2006, 01/2008
(Ting - 2s97, Léo - 1s2006)
Como se transforma um número representado na base decimal para
a base não-decimal b?
Dado um número inteiro, na base decimal, contendo n dígitos. Qual
deve ser a quantidade mínima de bits, m, para representá-lo na base binária?
O que é uma representação em complemento de b e em complemento de (b-1)
de um número na base b?
Como são codificados os números sem sinal em formato binário?
Por que a representação octal é bem menos utilizada
que a representação hexadecimal?
Quais são as vantagens e desvantagens do código BCD?
Como podem ser representados os números com sinal numa base b?
Seja 11100010 o conteúdo de um registrador de 8 bits. O que
este código binário representa, considerando que ele seja:
- uma representação sem sinal em código binário?
- uma representação com sinal e magnitude em código binário?
- uma representação com sinal e complemento de 1 em código binário?
- uma representação com sinal e complemento de 2 em código binário?
Por que a representação em complemento de 2 é considerada
a mais adequada
para implementação de operações aritméticas em circuitos digitais?
A adição (ou subtração) em ponto flutuante se faz do mesmo modo
que em ponto fixo?
Explicite todos os números que podem ser representados
exatamente considerando a representação numérica de ponto flutuante
normalizado com mantissa de 3 bits (codificada em sinal+magnitude) e
expoente de 3 bits (codificado em complemento de 2). Suponha ainda que a base
(implícita) seja 2.
Quais são os caracteres representáveis pelo código ASCII
(American Standard Code for Information Interchange)?
Seja 01100010 o conteúdo de um registrador de 8 bits. O que
este código binário representa, considerando que ele seja:
- um código hexadecimal?
- um código octal?
- um código BCD?
- uma representação em ponto fixo (bit mais significativo (7) = sinal,
bits 6-3 = parte inteira e bits 2-0 = parte fracionária, base = 2)?
- uma representação em ponto flutuante (bit mais significativo (7) = sinal,
bits 6-3 = mantissa e bits 2-0 = expoente em complemento de 2, base = 2)?
- um código ASCII (7 bits menos significativos)?
Como se transforma um número representado na base decimal para
a base não-decimal b?
Vimos na Seção VIII.1 do livro-texto que um número representado numa base não-decimal,
com n dígitos à esquerda da vírgula e m dígitos à direita,
pode ser transformado para a base decimal pela equação:
(N)10 = dígiton . bn +dígito(n-1) . b(n-1) + ...
+ dígito1 . b1 + dígito0 . b0 + dígito-1 . b-1 + ...
+ dígito-m . b-m .
Para a transformação inversa, isto é da base decimal para uma não-decimal,
podemos seguir o seguinte algoritmo:
- Separar o número em parte inteira e parte fracionária;
- Dividir a parte inteira I por b. Se o quociente
for zero, páre. Senão, substitua I pelo quociente
e continue a divisão sucessivamente. Os restos em cada divisão
são concatenados, na sequência de dígito menos significativo para
o mais significativo, para formar a parte inteira do resultado.
- Multiplicar a parte fracionária F por b.
Se a parte fracionária do produto for nula, páre. Senão
substitua F pela parte fracionária do produto
e continue a multiplicação sucessivamente. As partes inteiras
do produto em cada multiplicação são concatenadas,
na ordem de dígito mais próximo da vírgula para o mais
distante, para formar a parte fracionária do resultado.
Por exemplo, o número (241,1640625)10 é transformado
em (F1,2A)16 pelo seguinte procedimento:
| 241 |
|
|
|
0.1640625 |
| 15 |
1 |
1 |
|
x 16 |
| 0 |
15 |
F |
|
2.6250000 |
2 |
| |
|
|
|
x 16 |
| |
|
|
|
10.000000 |
A |
e o número (15,625)10 é transformado
em (1111,101)2 pelo seguinte procedimento:
| 15 |
|
|
|
0.625 |
| 7 |
1 |
1 |
|
x 2 |
| 3 |
1 |
1 |
|
1.250 |
1 |
| 1 |
1 |
1 |
|
x 2 |
| 0 |
1 |
1 |
|
0.500 |
0 |
| |
|
|
|
x 2 |
| |
|
|
|
1.000 |
1 |
Vale ressaltar aqui a observação feita na Seção VIII.3.2 do livro-texto de que a
transformação de números entre a base decimal e bases não-decimais
nem sempre permite uma representação
exata após a transformação.
Dado um número inteiro, na base decimal, contendo n dígitos. Qual
deve ser a quantidade mínima de bits, m, para representá-lo na base binária?
O valor m deve ser tal que satisfaça a seguinte desigualdade:
2m - 1
>= 10n - 1
<=>
2m >= 10n
<=>
log102m >= n
<=>
m.log102 >= n
<=>
0,30103.m >= n
<=>
m >= 3,3219.n.
O que é uma representação em complemento de b e em complemento de (b-1)
de um número na base b?
Dado um número N na base b, com n dígitos à esquerda da vírgula
e m dígitos à direita, o complemento de (b-1) de N é, por
definição,
bn - N - b-m
e o complemento de b de N é, por
definição,
bn - N.
Note que o complemento de b de N pode ser obtido adicionando
b-m ao complemento de (b-1) de N, uma vez que
bn - N = [bn - N - b-m] + b-m
Exemplos:
| Base b |
Número |
Complemento de b-1 |
Complemento de b |
| 2 |
011.011 |
100.100 |
100.101 |
| 8 |
05467.0 |
72310.7 |
72311.0 |
| 10 |
05467.00 |
94532.99 |
94533.00 |
| 16 |
0CD.31 |
F32.CE |
F32.CF |
Vale a pena ressaltar ainda que o complemento numérico do complemento de um
número N é o próprio N, pois
bn - (bn - N - b-m) - b-m = N
e
bn - (bn - N) = N.
Como são codificados os números sem sinal em formato binário?
A forma mais simples para codificar, em formato binário,
os números em qualquer base é
associar a cada dígito um grupo de bits suficientes para representar
cada dígito, ou seja,
| Base |
Número de bits |
| 2 (Binária) |
1 |
| 8 (Octal) |
3 |
| 10 (Decimal) |
4 |
| 16 (Hexadecimal) |
4 |
Se representarmos cada dígito por seu valor binário correspondente,
vimos na Seção VIII.1 do livro-texto que a transformação de números
entre a base binária e a base octal (hexadecimal) é imediata,
bastando agrupar os dígitos binários de 3 em 3 (4 em 4).
Dada uma sequência de dígitos binários 100011111100 que representa
um número na base binária, e número nas bases octal e
hexadecimal é representado, respectivamente, por (4374)8
e (8FC)16, como mostram as seguintes tabelas:
Em outras palavras, nesta forma de codificação, os formatos binários de um número b
na base binária, de um número o na base octal e de um número
h na base hexadecimal são extamente os mesmos, se e somente se
b, o e h denotam o mesmo valor numérico.
A forma mais natural para codificar cada dígito de um número
na base decimal por 4 bits é também representar cada dígito pelo
seu valor binário correspondente. Esta forma de codificação,
apresentada na Seção VIII.1 do livro-texto,
é conhecida como binary-coded decimal (código
BCD). Outra forma
de codificação, conhecida como código de Gray, é aquela
que modifica somente o valor de 1 bit entre dois dígitos decimais
subsequentes, conforme a tabela abaixo:
| Valor Decimal |
Binário Natural |
Código de Gray |
| 0 |
0000 |
0010 |
| 1 |
0001 |
0110 |
| 2 |
0010 |
0111 |
| 3 |
0011 |
0101 |
| 4 |
0100 |
0100 |
| 5 |
0101 |
1100 |
| 6 |
0110 |
1101 |
| 7 |
0111 |
1111 |
| 8 |
1000 |
1110 |
| 9 |
1001 |
1010 |
Por que a representação octal é bem menos utilizada
que a representação hexadecimal?
Porque as máquinas são comumente projetadas para operar os bits individualmente,
ou em "grupos" de 4, 8, 16, 32 ou 64 bits.
Quais são as vantagens e desvantagens do código BCD?
Embora o sistema binário seja o sistema mais apropriado para computadores,
códigos para sistemas decimais e operações para estes códigos têm sido
amplamente estudados devido à nossa familiaridade com este sistema numérico.
Entretanto, códigos decimais requerem um hardware mais complexo
para implementar as operações aritméticas e apresentam uma taxa menor
de aproveitamento do espaço de memória (4 bits são utilizados para
codificar 10 distintos dígitos decimais!)
Como podem ser representados os números com sinal numa base b?
Existem basicamente três tipos de representação de um número N
numa base b:
- sinal e magnitude de N;
- sinal e complemento de b;
- sinal e complemento de (b-1).
Como vimos na Seção VIII.1 do livro-texto, os três tipos de representação
só diferem na codificação de números negativos. Na representação por sinal e
magnitude, a representação de um número negativo é obtida complementando
somente o dígito mais significativo (o de sinal) da representação do número
positivo correspondente; enquanto na representação
por complemento numérico, a representação de um número negativo corresponde
ao seu complemento de b ou de (b-1), como mostram os seguintes
exemplos:
| Base (b) |
Sinal e Magnitude |
Sinal e Complemento de b |
Sinal e Complemento de b-1 |
| 16 |
0 F1.A7 |
0 F1.A7 |
0 F1.A7 |
| 16 |
F F1.A7 |
F 0E.59 |
F 0E.58 |
| 10 |
0 14.37 |
0 14.37 |
0 14.37 |
| 10 |
9 14.37 |
9 85.63 |
9 85.62 |
| 8 |
0 14.37 |
0 14.37 |
0 14.37 |
| 8 |
7 14.37 |
7 63.41 |
7 63.40 |
| 2 |
0 1110.011 |
0 1110.011 |
1 1110.011 |
| 2 |
1 1110.011 |
1 0001.101 |
1 0001.100 |
Seja 11010010 o conteúdo de um registrador de 8 bits. O que
este código binário representa, considerando que ele seja:
- uma representação sem sinal em código binário?
- uma representação com sinal e magnitude em código binário?
- uma representação com sinal e complemento de 1 em código binário?
- uma representação com sinal e complemento de 2 em código binário?
- Representação sem sinal em código binário: 27+26+24+21 = 210.
- Representação com sinal e magnitude:-(26+24+21) = -82.
- Representação com sinal e complemento de 1: Descartando o bit de sinal
(1010010) é o complemento de 1 de (0101101)2 =
(45)10.
- Representação com sinal e complemento de 2: Descartando o bit de sinal
(1010010) - 1 = (1010001) é o complemento de 1 de
(0101110)2 = (46)10.
Por que a representação em complemento de 2 é considerada
a mais adequada
para implementação de operações aritméticas em circuitos digitais?
A representação em complemento numérico permite tratar uniformemente
as operações aritméticas entre os números positivos e negativos.
Vimos, por exemplo,
no faq2 que, para representações em complemento de 2,
uma subtração entre dois números
pode ser reduzida às operações de soma e de complemento dos dígitos.
O sinal do resultado da soma entre dois números em complemento de dois
é também derivado de forma bastante natural, como exemplificam
as duas somas seguintes:
| +8 |
0 00001000 |
|
+8 |
0 00001000 |
| +14 |
0 00001110 |
|
-14 |
1 11110010 |
| ---- |
---------- |
|
--- |
---------- |
| +22 |
0 00010110 |
|
-6 |
1 11111010 |
Podemos ainda utilizar o mesmo circuito de adição para subtrair dois
números com sinal lembrando que:
(sA) - (+B) = (sA) + (-B)
(sA) - (-B) = (sA) + (+B),
onde s denota o sinal negativo ou positivo.
Além disso, a multiplicação entre dois números com sinal pode ser, com uso
do algoritmo de Booth, uniformemente tratada para valores positivos e negativos. Este algoritmo se
baseia no fato de que o multiplicador é decomponível em
soma de números, com sinal e múltiplos de 2 (isto é,
2i ou -2i,
sendo i o i-ésimo dígito do multiplicador)
e o resultado da
multiplicação ser a soma das multiplicações parciais entre o
multiplicando e cada um desses números. A escolha por (2i) ou
(-2i) depende da transição entre os dígitos ai e
a(i-1)
no multiplicador ao varrê-lo da direita para a esquerda. Considerando sempre
a-1 = 0, temos:
| aia(i-1) |
Multiplicador Parcial |
| 00 |
0 |
| 01 |
2i |
| 10 |
-2i |
| 11 |
0 |
Para exemplificar faremos a multiplicação de dois números, +4 e (-5),
representados em complemento de 2.
| +4 |
|
0100 |
|
multiplicando |
| x -5 |
|
x 1011 |
|
multiplicador |
| ---- |
|
------- |
|
|
| |
|
11111100 |
|
padrão 10 <<<<<< (-20 x 0100) |
| |
|
0000000 |
|
padrão 11 <<<<<< (00000000) |
| |
|
000100 |
|
padrão 01 <<<<<< (+22 x 0100) |
| |
|
11100 |
|
padrão 10 <<<<<< (-23 x 0100) |
| |
|
------- |
|
|
| |
|
11101100 |
|
resultado (-20) |
Finalmente, a divisão entre dois números com sinal pode ser sempre
reduzida a uma sequência sucessiva de comparações, deslocamentos e subtrações.
E a implementação dessas operações em circuitos digitais é relativamente simples
para representações em complemento de 2.
Vale ressaltar aqui que os algoritmos apresentados são aplicáveis para
representações em ponto fixo.
A adição (ou subtração) em ponto flutuante se faz do mesmo modo
que em ponto fixo?
Não. Em representação que utiliza ponto flutuante, não é possível
realizar a adição (ou subtração) com exponentes diferentes.
Os seguintes passos devem ser adotados:
- identificar o número com o menor expoente;
- fazer o menor expoente igual ao maior expoente pela divisão da
mantissa pelo mesmo fator utilizado para aumentar o expoente;
- adicionar (ou subtrair) as mantissas; e
- se necessário, normalizar o resultado.
Explicite todos os números que podem ser representados
exatamente considerando a representação numérica de ponto flutuante
normalizado com mantissa de 3 bits (codificada em sinal+magnitude) e
expoente de 3 bits (codificado em complemento de 2). Suponha ainda que a base
(implícita) seja 2.
Representação:
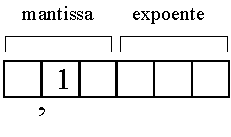
Combinações possíveis para a mantissa:
| 0,10 |
0,11 |
1,10 |
1,11 |
| +0,5 |
+0,75 |
-0,5 |
-0,75 |
Combinações possíveis para o expoente
| 000 |
001 |
010 |
011 |
111 |
110 |
101 |
100 |
| 0 |
+1 |
+2 |
+3 |
-1 |
-2 |
-3 |
-4 |
Números representáveis (como são simétricos só foram representados os pontos na semi-reta
positiva:
 Observe que
Observe que
- como são 5 bits, somente 32 números da reta real
são exatamente representáveis;
- o espaçamento entre os números representáveis
varia ao longo da reta real. Quanto menor for o expoente
(mais próximos forem os números de zero),
menor é o espaçamento.
Compare, por exemplo, a distância
entre 0.75 x 23 e 0.5 x 23 com a
distância entre 0.75 x 2-3 e 0.5 x 2-3
na reta real;
- a precisão na faixa be, onde b e
e são respectivamente
base e expoente, é a mesma (isto é, o espaçamento
entre os números, de mesmo
sinal e com o mesmo valor de expoente, é o mesmo).
Acrescente um bit à mantissa e compare, por exemplo,
a distância entre 0.75 x 22 (0110010)
e 0.625 x 22 (0101010) e a distância entre
0.5 x 22 (0100010) e 0.625 x 22 (0101010);
- a precisão depende
da faixa de valores representáveis pela mantissa
(número de bits no campo de mantissa). Quanto maior for
a faixa de valores da mantissa, maior é o número
de pontos representáveis no intervalo
[0.5,1.0)xbe, onde b e
e são, respectivamente,
base e expoente; (Tente passar um bit do campo de expoente
para o campo de mantissa ...)
- a faixa de representação depende
da faixa de valores representáveis pelo expoente
(número de bits no campo de expoente). Quanto maior for
a faixa de valores do expoente, mais espalhados estariam
os 32 números exatamente representáveis
sobre a reta real; (Tente passar um bit do campo de mantissa
para o campo de expoente ...)
- a representação de zero não pode ser normalizada, uma
vez que ele não contém nenhum dígito não nulo. Em
alguns computadores (que não utilizam bit escondido),
ele é representado através de zero's tanto no campo da
mantissa como no do expoente.
Quais são os caracteres representáveis pelo código ASCII
(American Standard Code for Information Interchange)?
Código binário ASCII (ISO - 7 bits)
| |
b6b5b4 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| b3b2b1b0 |
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
| 0 |
0000 |
Null |
Data link escape (DLE) |
Space (SP) |
0 |
@ |
P |
‘ |
p |
| 1 |
0001 |
Start of heading (SOH) |
Device control 1 (DC1) |
! |
1 |
A |
Q |
a |
q |
| 2 |
0010 |
Start of text (STX) |
Device control 2 (DC2) |
² |
2 |
B |
R |
b |
r |
| 3 |
0011 |
End of text (ETX) |
Device control 3 (DC3) |
# |
3 |
C |
S |
c |
s |
| 4 |
0100 |
End of Transmission (EOT) |
Device control 4 (DC4) |
$ |
4 |
D |
T |
d |
t |
| 5 |
0101 |
Enquiry (ENQ) |
Negative aknowledge (NAK) |
% |
5 |
E |
U |
e |
u |
| 6 |
0110 |
Acknowledge (ACK) |
Synchronous idle (SYN) |
& |
6 |
F |
V |
f |
v |
| 7 |
0111 |
Bell (BEL) |
End of transmission block (ETB) |
' |
7 |
G |
W |
g |
w |
| 8 |
1000 |
Backspace (BS) |
Cancel (CAN) |
( |
8 |
H |
X |
h |
x |
| 9 |
1001 |
Horizontal tab (HT) |
End of medium (EM) |
) |
9 |
I |
Y |
i |
y |
| A |
1010 |
Line feed (LF) |
Substitute (SUB) |
* |
: |
J |
Z |
j |
z |
| B |
1011 |
Vertical tab (VT) |
Escape (ESC) |
+ |
; |
K |
[ |
k |
{ |
| C |
1100 |
Form feed (FF) |
File separator (FS) |
, |
< |
L |
\ |
l |
| |
| D |
1101 |
Carriage return (CR) |
Group separator (GS) |
- |
= |
M |
] |
m |
} |
| E |
1110 |
Shift out (SO) |
Record separator (RS) |
. |
= |
N |
^ |
n |
~ |
| F |
1111 |
Shift in (SI) |
Unit separator (US) |
/ |
? |
O |
_ |
o |
Delete (DEL) |
| |
|
Caracteres de controle |
Caracteres imprimíveis |
O código ASCII compreende 128 caracteres. Cada caracter é representado por 7 bits
b6b5b4b3b2b1b0.
O oitavo bit pode ser zerado, ou utilizado como bit de paridade.
Observe que
- os 4 bits menos significativos dos códigos dos digitos decimais
correspondem ao código BCD. Isso facilita
a comparação entre dois dígitos e a conversão entre os dois
códigos; e
- os códigos binários que representam caracteres A-Z e a-z estão
em ordem crescente. Isso facilita a ordenação de caracteres.
Seja 01101110 o conteúdo de um registrador de 8 bits. O que
este código binário representa, considerando que ele seja:
- um código hexadecimal?
- um código octal?
- um código BCD?
- uma representação em ponto fixo (bit mais significativo (7) = sinal,
bits 6-3 = parte inteira e bits 2-0 = parte fracionária, base = 2)?
- uma representação em ponto flutuante (bit mais significativo (7) = sinal,
bits 6-3 = mantissa e bits 2-0 = expoente em complemento de 2, base = 2)?
- um código ASCII (7 bits menos significativos)?
- Código Hexadecimal: (6E)H = (110)10, pois
- Código Octal: adicionando um dígito 0 à esquerda, temos (156)8=(110)10, uma vez que
Observe que, como já mencionado no item anterior,
o valor numérico é o mesmo para a representação octal e a hexadecimal.
- Código BCD: não tem sentido, uma vez que os 4 bits menos significativos não
correspondem a um padrão do código BCD.
- Ponto Fixo:
- Sinal: 0 (positivo)
- Parte Inteira: 1101
- Parte Fracionária: 110
23 + 22 + 20 + 2-1 + 2-2=13,75.
- Ponto Flutuante:
- Sinal: 0 (positivo)
- Mantissa: 0.1101
- Expoente: 110
Como a representação do expoente é complemento de 2, então o seu valor é (-2).
O número representado é, portanto, 0.1101 x 2-2.
- Código ASCII: Pela tabela de ASCII o código corresponde
à letra minúscula n.
Last modified: mon Apr 24 23:10:29 BRA 2008
Sugestões para leopini@dca.fee.unicamp.br
Voltar para a página do curso.