Estimating elements of discrete differential geometry on the GPU

Harlen Costa Batagelo
Wu, Shin-Ting

Department of Industrial Automation and Computer Engineering (DCA)
School of Electrical and Computer Engineering (FEEC)
State University of Campinas (UNICAMP)

The estimation of differential geometry quantities from discrete surfaces has been widely used in geometric modeling and computer vision applications such as object segmentation, shape analysis and anisotropic mesh fairing. Besides the estimation of vertex normals and tangents, today's real-time shader techniques may require the per-vertex computation of 2nd or 3rd order differential quantities of meshes, such as the tensor of curvature and tensor of curvature derivative. In particular, principal directions and curvatures are required for shaders that simulate silhouettes of mesostructure details. In non-photorealistic rendering, the computation of “suggestive contours” may be obtained from using the tensor of curvature derivative. Also, hatching based on object-space coherence may rely on the principal directions to improve the perception of shape. The estimation of elements of discrete differential geometry may also be used in the context of interaction by direct manipulation. For instance, in a 3D painting application, the principal directions may help the user in guiding the brush on the surface. Moreover, the curvatures may be used in the evaluation of the gravity function of a surface snapping technique.

We have developed a GPU-friendly technique for the estimation of 2nd and 3rd order elements of differential geometry from arbitrary triangle meshes or point clouds with 1-ring connectivity information. The technique is scaled to SM 3.0 GPUs using a general-purpose stream processing approach, and can be used to compute the tensor of curvature, principal curvatures, principal directions, Gaussian curvature, mean curvature and tensor of curvature derivative. Since it works in real-time, it can be used with meshes under non-rigid body transformations.

Downloads

Estimating Curvatures and their Derivatives on Meshes of Arbitrary Topology from Sampling Directions (3.17 MB, in PDF)
Presented in CGI 2007. To appear in The Visual Computer.
Disclaimer: This is an author-created version of the paper. The original publication is available at www.springer.link.com.

Demonstration with source code (13.3 MB)

Minimum requirements and licensing

The executable requires MS DirectX 9.0c Runtime and a graphics board with support to Shader Model 3.0 and floating point render targets. The source code was created with MS Visual Studio .NET 2002 and is released under the LGPL license:

Copyright (C) 2007 Harlen Costa Batagelo

This library is free software; you can redistribute it and/or
modify it under the terms of the GNU Lesser General Public
License as published by the Free Software Foundation; either
version 2.1 of the License, or (at your option) any later version.

This library is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
Lesser General Public License for more details.

Screenshots

Visualization of the principal curvatures as colors. The bottom-right box shows the color-coded scheme of the principal curvatures according to their signals (k1 is the minimum curvature; k2 is the maximum curvature).

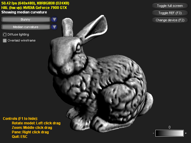
Grayscale visualization of the Gaussian curvature: K=k1*k2
The surface is locally hyperbolic when K<0, parabolic/planar when K=0, and elliptical when K>0.

Visualization of the mean curvature H=(k1+k2)/2
The points in which H=0 correspond to locally minimal regions.

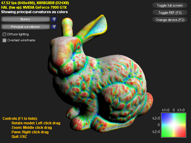
Visualization of the principal directions. The red axis points to the (tangent) direction of the minimum curvature. The green axis points to the direction of the maximum curvature.

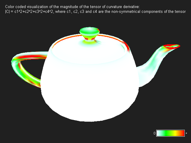
Color-coded visualization of the magnitude of the tensor of curvature derivative: |C|=c1^2+c2^2+c3^2+c4^2, where c1, c2, c3 and c4 are the non-symmetrical components of the tensor.

Color-coded principal curvatures on a knot.

Principal directions on a knot.

Mean curvature on the Stanford bunny.

Color-coded principal curvatures on the Stanford bunny.